Wiener Trial

Dois exemplos de caminhos de um processo Wiener padrão

Um processo Wiener (em homenagem ao matemático americano Norbert Wiener ) é um processo estocástico contínuo no tempo que tem aumentos normalmente distribuídos e independentes . Ele representa um modelo matemático para o movimento browniano e, portanto, é freqüentemente referido como o próprio "movimento browniano".

Desde a introdução da análise estocástica por Itō Kiyoshi na década de 1940, o processo Wiener desempenhou um papel central no cálculo de processos estocásticos contínuos no tempo e em muitas áreas das ciências naturais e econômicas serve como base para modelar desenvolvimentos aleatórios.

história

Thorvald N. Thiele

Louis Bachelier

Em 1827, o botânico escocês Robert Brown observou sob o microscópio como o pólen das plantas se movia irregularmente para frente e para trás em uma gota d'água (daí o nome movimento browniano ).

1880 descreveu o estatístico e astrônomo Thorvald N. Thiele (1838-1910) em Copenhague pela primeira vez um tal "processo" (a teoria dos processos estocásticos ainda não havia sido desenvolvida) quando as séries econômicas e a distribuição dos resíduos no método dos mínimos quadrados estudados. Em 1900, o matemático francês Louis Bachelier (1870-1946), aluno de Henri Poincaré , retomou a ideia de Thiele quando tentava analisar os movimentos dos preços na bolsa de Paris . Em última análise, ambas as abordagens tiveram pouco impacto no desenvolvimento futuro do processo, em parte porque a matemática financeira desempenhou um papel secundário na matemática da época; hoje, entretanto, é considerada a principal área de aplicação dos julgamentos vienenses. Ainda preferido z. B. o estocástico William Feller chamou o processo de Bachelier-Wiener .

A descoberta veio quando Albert Einstein, em seu annus mirabilis em 1905 , aparentemente sem conhecimento do trabalho de Bachelier, e independentemente dele, Marian Smoluchowski definiu o Julgamento de Viena em sua forma atual em 1906. A motivação de Einstein era explicar o movimento das partículas brownianas através da estrutura molecular da água - uma abordagem que era extremamente controversa na época, mas agora é indiscutível - e apoiar essa explicação matematicamente. Curiosamente, ele não pedir para outro, fisicamente propriedade significativa, o rectifiability dos caminhos aleatórios , para seu modelo. Embora isso signifique que as partículas percorram uma distância infinitamente longa a cada segundo (o que teoricamente desqualifica todo o modelo), a abordagem de Einstein significou um avanço tanto para a teoria molecular quanto para o processo estocástico.

Einstein, porém, não forneceu qualquer prova da existência probabilística do processo. Isso não foi alcançado até 1923 pelo matemático americano Norbert Wiener , que foi capaz de usar novas ferramentas de Lebesgue e Borel no campo da teoria da medida . No entanto, sua prova era tão longa e complicada que apenas um punhado de contemporâneos poderia entendê-la. Diz-se que Ito Kiyoshi fez alguns de seus maiores avanços no desenvolvimento da integral estocástica ao tentar entender o trabalho de Wiener.

Em última análise, foi Itō quem abriu o caminho para o processo de Wiener da física para outras ciências: as equações diferenciais estocásticas que ele estabeleceu tornaram possível adaptar o movimento browniano a problemas mais estatísticos. O movimento browniano geométrico derivado de uma equação diferencial estocástica resolve o problema de que o processo de Wiener, independente de seu valor inicial, quase certamente atinge valores negativos com o passar do tempo, o que é impossível para ações; A abordagem de Bachelier acabou falhando. Desde o desenvolvimento do famoso modelo Black-Scholes , o movimento geométrico browniano tem sido considerado o padrão.

O problema levantado pelos caminhos não retificáveis ​​do processo de Wiener na modelagem de caminhos brownianos leva ao processo de Ornstein-Uhlenbeck e também deixa clara a necessidade de uma teoria de integração e diferenciação estocástica - aqui, não é o movimento, mas a velocidade da partícula considerada como um processo retificável modelado derivado do processo de Wiener, a partir do qual os caminhos retificáveis ​​das partículas são obtidos por integração.

Hoje, em praticamente todas as ciências naturais e muitas ciências sociais, os movimentos brownianos e processos relacionados são usados ​​como ferramentas.

definição

Um processo Wiener é um processo estocástico contínuo no tempo que tem aumentos normalmente distribuídos e independentes:
Um processo estocástico no espaço de probabilidade é chamado de processo Wiener (padrão) se as seguintes quatro condições se aplicarem: ${\ displaystyle (W_ {t}) _ {t \ in \ mathbb {R} _ {+}}}$ ${\ displaystyle (\ Omega, {\ mathcal {A}}, P)}$

1. ${\ displaystyle W_ {0} = 0}$(P- quase certo ).
2. Para determinados pontos no tempo , os aumentos são estocasticamente independentes . O Processo de Viena, portanto, tem ganhos independentes.${\ displaystyle 0 \ leq t_ {0} <t_ {1} <t_ {2} <\ dotsb <t_ {m}}$${\ displaystyle W_ {t_ {1}} - W_ {t_ {0}}, W_ {t_ {2}} - W_ {t_ {1}}, \ dotsc, W_ {t_ {m}} - W_ {t_ { m-1}}}$
3. Para tudo verdade . Os aumentos são estacionários e normalmente distribuídos com o valor esperado zero e a variância .${\ displaystyle 0 \ leq s <t}$${\ displaystyle W_ {t} -W_ {s} \; \ sim \; {\ mathcal {N}} \ left (0, ts \ right)}$ ${\ displaystyle ts}$
4. Os caminhos individuais são (P-) quase certamente contínuos .

O quarto ponto também pode ser excluído da definição, na medida em que pode ser mostrado com o teorema da continuidade de Kolmogorow-Tschenzow que sob o acima mencionado É quase certo que sempre há uma versão estável do processo .

Alternativamente, um processo Wiener de acordo com Paul Lévy pode ser caracterizado pelas duas propriedades a seguir: ${\ displaystyle (W_ {t}) _ {t \ in \ mathbb {R} _ {+}}}$

1. ${\ displaystyle W_ {t}}$é um martingale local estável com .${\ displaystyle W_ {0} = 0}$
2. ${\ displaystyle {W_ {t}} ^ {2} -t}$ é um martingale.

propriedades

classificação

• O processo Wiener pertence à família dos processos de Markov e, especificamente, à classe dos processos de Levy . Além disso, cumpre a forte qualidade de Markov .
• O processo de Wiener é um processo gaussiano especial com uma função de valor esperado e uma função de covariância .${\ displaystyle \ operatorname {E} (W_ {t}) = 0}$ ${\ displaystyle \ operatorname {Cov} (W_ {s}, W_ {t}) = \ min (s, t)}$
• O Julgamento de Viena é um martingale . Portanto, se a filtragem produzida por , a expectativa condicional se aplica a todos .${\ displaystyle ({\ mathcal {F}} _ {t}) _ {t \ geq 0}}$${\ displaystyle (W_ {t}) _ {t \ geq 0}}$ ${\ displaystyle E (W_ {t} \ mid {\ mathcal {F}} _ {s}) = W_ {s}}$${\ displaystyle 0 \ leq s <t}$
• O processo Wiener é um processo Lévy com caminhos contínuos e valor esperado constante .${\ displaystyle 0}$

Propriedades dos caminhos

• Os caminhos de um processo de Wiener quase certamente não são diferenciáveis em nenhum ponto ( teorema de Paley-Wiener-Zygmund ) e quase certamente não retificáveis .
• Os caminhos quase certamente têm variação infinita em cada intervalo .${\ displaystyle [s, t] \ subset \ mathbb {R} _ {+}}$
• Para a variação quadrática, é quase certo que seja verdade .${\ displaystyle [W, W] _ {t} = \ langle W, W \ rangle _ {t} = t}$
• As leis do logaritmo iterado fornecem informações sobre assintóticos no infinito e em torno do ponto zero .
• O seguinte se aplica a um julgamento vienense${\ displaystyle (W_ {t}) _ {t \ geq 0}}$

${\ displaystyle \ limsup _ {h \ rightarrow 0} \ left ({\ frac {\ sup _ {t \ in [0, h]} | W_ {t + h} -W_ {t} |} {(2h \ log ({\ frac {1} {h}})) ^ {\ frac {1} {2}}}} \ right) = 1}$

com certeza. Assim, os caminhos do processo de Wiener são, em particular , contínuos de Hölder ao expoente com , mas não para .${\ displaystyle \ alpha}$${\ displaystyle \ alpha <{\ frac {1} {2}}}$${\ displaystyle \ alpha = {\ frac {1} {2}}}$

Auto-semelhanças, princípio de reflexão

• Também é o negativo de um processo Wiener padrão, portanto, é um processo Wiener padrão. O princípio da reflexão também se aplica de forma mais geral : um processo vienense espelhado em qualquer momento de parada é novamente um processo vienense. O processo espelhado é definido da seguinte forma: se e se .${\ displaystyle (-W_ {t}), \; t \ geq 0,}$ ${\ displaystyle \ tau}$${\ displaystyle {\ hat {W}} _ {t}}$${\ displaystyle {\ hat {W}} _ {t} (\ omega) = W_ {t} (\ omega)}$${\ displaystyle t \ leq \ tau (\ omega)}$${\ displaystyle {\ hat {W}} _ {t} (\ omega) = 2W _ {\ tau (\ omega)} (\ omega) -W_ {t} (\ omega)}$${\ displaystyle t> \, \ tau (\ omega)}$
• O processo de Wiener é semelhante ao alongamento do eixo do tempo, i. H. é um processo vienense padrão para todos.${\ displaystyle X_ {t} = {\ tfrac {1} {\ sqrt {\ alpha}}} \ cdot W _ {\ alpha \ cdot t}}$${\ displaystyle \ alpha> 0}$
• Inversão do eixo do tempo: também é um processo Wiener padrão${\ displaystyle X_ {t} = tW _ {\ frac {1} {t}}}$
• Mudando o eixo do tempo: para todo determinístico , o processo estocástico também é um processo de Wiener; aqui, os aumentos são considerados a partir do ponto no tempo , i. H. cumpre a fraca propriedade de Markov.${\ displaystyle s \ geq 0}$${\ displaystyle X_ {t} = W_ {t + s} -W_ {s}}$${\ displaystyle s}$${\ displaystyle W}$

gerador

Um movimento amarronzado na esfera. O gerador desse processo é ½ vezes o operador Laplace-Beltrami em um manifold, aqui uma superfície esférica.

O seguinte se aplica ao gerador de um processo Wiener padrão unidimensional ${\ displaystyle A}$

${\ displaystyle Af (x) = \ lim \ limits _ {t \ downarrow 0} {\ frac {E (f (x + W_ {t})) - f (x)} {t}} = {\ frac { 1} {2}} f '' (x)}$,

isto é , ½ vezes o operador da segunda derivada. De maneira mais geral, o gerador de um processo Wiener multidimensional é ½ vezes o operador Laplace . Esta relação pode ser usada para aplicar processos Wiener a outras variedades , como B. a definir numa esfera (ver imagem), nomeadamente como um processo de Markov com o operador Laplace-Beltrami como gerador. ${\ displaystyle A}$

Processo Wiener generalizado

Se um processo Wiener padrão é chamado de processo estocástico ${\ displaystyle (W_ {t})}$

${\ displaystyle X_ {t} = \ mu t + \ sigma W_ {t}}$

Movimento browniano com deriva e volatilidade . Isso também permite que os processos estocásticos a ser representados que tendem a cair ( ) ou tendem a aumentar ( ). O seguinte se aplica aqui ${\ displaystyle \ mu}$${\ displaystyle \ sigma}$${\ displaystyle \ mu <0}$${\ displaystyle \ mu> 0}$

${\ displaystyle X_ {t} -X_ {s} \ sim {\ mathcal {N}} \ left (\ mu (ts), \ sigma ^ {2} \ left (ts \ right) \ right)}$.

Os processos gerais de Wiener também são processos de Markov e Lévy, mas a propriedade martingale só é válida em uma forma enfraquecida:

É por isso é um super- martingale , é assim é uma submartingale . Pois é um martingale . ${\ displaystyle \ mu \ leq 0}$${\ displaystyle X_ {t}}$${\ displaystyle \ mu \ geq 0}$${\ displaystyle X_ {t}}$${\ displaystyle \ mu = 0}$${\ displaystyle X_ {t}}$

O caso multidimensional

75 passos de uma aproximação discreta para um movimento browniano bidimensional. A partícula poderia ter se movido de maneira semelhante sob o microscópio de Brown.

Um processo estocástico multidimensional é chamado de processo Wiener n-dimensional (padrão) ou movimento Browniano n-dimensional se as coordenadas forem processos Wiener independentes (padrão). Os aumentos são então também independentes e distribuídos (distribuição normal n-dimensional ), onde a matriz unitária da dimensão é n . ${\ displaystyle W_ {t} = (W_ {1, t}, W_ {2, t}, \ ldots W_ {n, t}) ^ {T}, \; t \ geq 0}$${\ displaystyle (W_ {i, t})}$ ${\ displaystyle W_ {t} -W_ {s}}$${\ displaystyle {\ mathcal {N}} (0, (ts) I_ {n})}$${\ displaystyle I_ {n}}$

O processo n-dimensional de Wiener tem uma propriedade particularmente bela que o diferencia da maioria dos outros processos multidimensionais e que o predestina para modelar a partícula browniana: ele é invariável quando os eixos coordenados são girados. Isso significa que para cada matriz ortogonal o processo girado (ou espelhado) tem exatamente a mesma distribuição que . ${\ displaystyle Q \ in \ mathbb {R} ^ {n \ times n}}$${\ displaystyle X_ {t}: = QW_ {t}, \; t \ geq 0}$${\ displaystyle W_ {t}}$

Assim como o movimento browniano unidimensional, pode-se agora generalizar também o movimento n-dimensional: para cada vetor e cada matriz , torna-se através ${\ displaystyle \ mu \ in \ mathbb {R} ^ {n}}$${\ displaystyle A \ in \ mathbb {R} ^ {n \ times n}}$

${\ displaystyle X_ {t}: = \ mu t + AW_ {t}, \; t \ geq 0}$

define um movimento browniano com deriva e variância . O seguinte se aplica em conformidade . As coordenadas individuais também podem ser correlacionadas umas com as outras . ${\ displaystyle \ mu}$${\ displaystyle AA ^ {T}}$${\ displaystyle X_ {t} \ sim {\ mathcal {N}} (\ mu t, tAA ^ {T})}$

Relação com outros processos estocásticos

• Se há um movimento browniano geométrico , então é um movimento browniano (com deriva). Por outro lado, pode-se ganhar em qualquer processo vienense com deriva e volatilidade por meio de um movimento browniano geométrico.${\ displaystyle (X_ {t}) _ {t \ geq 0}}$${\ displaystyle W_ {t}: = \ ln (X_ {t})}$${\ displaystyle (X_ {t}) _ {t \ geq 0}}$${\ displaystyle \ mu}$${\ displaystyle \ sigma}$${\ displaystyle Y_ {t}: = \ mathrm {e} ^ {X_ {t} - {\ frac {\ sigma ^ {2} t} {2}}}}$
• Com a ajuda do termo integral estocástico de Itô, o processo de Wiener pode ser generalizado para o processo de Itō .
• O passeio aleatório simétrico pode ser considerado um equivalente em tempo discreto do processo de Wiener, porque é o seguinte teorema de convergência: para o passeio aleatório na grade de tempo discreta definida de modo que válido e em cada intervalo de tempo com probabilidade para cima e provável de move para baixo, então converge para um processo de Wiener padrão (para o tipo de convergência, consulte o princípio de invariância de Donsker ).${\ displaystyle n \ in \ mathbb {N}}$${\ displaystyle (R_ {t}) _ {t \ in T}}$${\ displaystyle T = \ left \ {0, {\ tfrac {1} {n}}, {\ tfrac {2} {n}}, \ ldots \ right \}}$${\ displaystyle R_ {0} = 0}$${\ displaystyle R}$${\ displaystyle 1/2}$${\ displaystyle {\ sqrt {\ tfrac {1} {n}}}}$${\ displaystyle 1/2}$${\ displaystyle {\ sqrt {\ tfrac {1} {n}}}}$${\ displaystyle R}$${\ displaystyle n \ to \ infty}$
• Se e é um processo padrão vienense , então é uma ponte browniana .${\ displaystyle (W_ {t}) _ {t \ geq 0}}$${\ displaystyle T> 0}$${\ displaystyle B_ {t}: = W_ {t} - {\ tfrac {t} {T}} W_ {T}, \ 0 \ leq t \ leq T}$

Simulação de caminhos brownianos

Vários métodos estão disponíveis para simular caminhos de um processo de Wiener com a ajuda de números aleatórios , todos baseados em diferentes propriedades do processo:

Passeio aleatório simples

A possibilidade mais simples é usar a convergência mencionada acima do passeio aleatório simples contra um processo de Wiener. Para isso, basta simular as variáveis ​​aleatórias B ₁ , B ₂ , B ₃ , ... distribuídas por Rademacher , que são independentes umas das outras e cada uma com probabilidade de assumir os valores 1 e −1. Em seguida, pode-se em um passo predeterminado um processo Wiener nos locais por ${\ displaystyle {\ tfrac {1} {2}}}$${\ displaystyle \ Delta t \ geq 0}$${\ displaystyle 0, \; \ Delta t, \; 2 \, \ Delta t, \; 3 \, \ Delta t \ ldots}$

${\ displaystyle W_ {n \ Delta t} \ approx {\ sqrt {\ Delta t}} \ sum _ {i = 1} ^ {n} B_ {i}}$

aproximado. A vantagem desse método é que apenas variáveis ​​aleatórias distribuídas pelo rademacher que são muito fáceis de produzir são necessárias. No entanto, é apenas uma aproximação: o resultado não é um processo gaussiano, mas tem estados quase binomialmente distribuídos (mais precisamente, é binomialmente (n; 0,5) -distribuído). Para aproximar suficientemente bem a distribuição normal, a escolha deve ser muito pequena. Portanto, este método só é recomendado se você quiser simular o processo em uma grade de tempo muito fina de qualquer maneira. ${\ displaystyle {\ frac {1} {2}} \ left (\ sum _ {i = 1} ^ {n} B_ {i} + n \ right)}$${\ displaystyle \ Delta t}$

Gaussian Random Walk

O método a seguir é superior ao passeio aleatório simples (a menos que uma grade de tempo particularmente fina seja necessária), uma vez que simula o processo exatamente (ou seja, os estados resultantes têm a mesma distribuição que os de um processo de Wiener):

${\ displaystyle W_ {n \ Delta t} \ approx {\ sqrt {\ Delta t}} \ sum _ {i = 1} ^ {n} Z_ {i}}$,

onde são números aleatórios padrão normalmente distribuídos independentes (por exemplo, gerados pelo método Polar de Marsaglia ). Esta discretização, conhecida como passeio aleatório Gaussiano , só é desvantajosa se as variáveis ​​aleatórias normalmente distribuídas presentes não forem de “qualidade” uniforme. Por exemplo, ao usar números quase aleatórios, os números que aparecem atrasados ​​às vezes têm estruturas de dependência que podem distorcer o resultado. Nesse caso, um dos seguintes métodos é preferível: ${\ displaystyle Z_ {1}, \; Z_ {2}, \; Z_ {3} \ ldots}$

Ponte browniana

As primeiras cinco etapas de divisão pela metade da ponte de Brown, a nova iteração simulada é mostrada em vermelho.

Este método, que remonta a Paul Lévy (que só marginalmente tem algo a ver com o estocástico processo da ponte browniano ) usa a estrutura de covariância do processo de Wiener e coloca maior ênfase na variáveis aleatórias normais início padrão . ${\ displaystyle Z_ {1}, Z_ {2}, \ ldots}$

Primeiro , que é normalmente distribuído com variância 1, é simulado por. Agora o intervalo é reduzido pela metade, passo a passo, e a seguinte etapa é repetida: ${\ displaystyle W_ {1}}$${\ displaystyle W_ {1} = Z_ {1}}$${\ displaystyle [0,1]}$

${\ displaystyle W _ {\ frac {1} {2}}}$resultados como a média aritmética mais outra variável aleatória normalmente distribuída para corrigir a variância. Então: ${\ displaystyle {\ frac {1} {2}} (W_ {0} + W_ {1})}$

${\ displaystyle W _ {\ frac {1} {2}} = {\ frac {1} {2}} (W_ {0} + W_ {1}) + {\ frac {1} {2}} Z_ { 2}}$

Análogo:

${\ displaystyle {\ begin {align} W _ {\ frac {1} {4}} & = {\ frac {1} {2}} (W_ {0} + W _ {\ frac {1} {2} }) + {\ frac {1} {\ sqrt {8}}} Z_ {3} \\ W _ {\ frac {3} {4}} & = {\ frac {1} {2}} (W _ {\ frac {1} {2}} + W_ {1}) + {\ frac {1} {\ sqrt {8}}} Z_ {4} \\ W _ {\ frac {1} {8}} & = {\ frac {1} {2}} (W_ {0} + W _ {\ frac {1} {4}}) + {\ frac {1} {4}} Z_ {5} \ end {alinhados} }}$

e assim por diante. Os fatores são reduzidos pelo fator em cada etapa de redução pela metade e garantem que os estados recebam a variação correta. ${\ displaystyle {\ tfrac {1} {2}}, \; {\ tfrac {1} {\ sqrt {8}}}, \; {\ tfrac {1} {4}} \ ldots}$${\ displaystyle {\ sqrt {2}}}$

Para estender um processo de Wiener a um intervalo arbitrário em vez de a um intervalo arbitrário , pode- se agora aplicar a transformação descrita acima ; um julgamento vienense está então em andamento . ${\ displaystyle [0,1]}$${\ displaystyle [0, a]}$${\ displaystyle X_ {t} = {\ sqrt {a}} W _ {\ frac {t} {a}}}$${\ displaystyle X}$${\ displaystyle [0, a]}$

O pano de fundo para essa modelagem não causal é que ela é condicionalmente e, novamente, normalmente distribuída. ${\ displaystyle W _ {(t_ {0} + t_ {1}) / 2}}$${\ displaystyle W_ {t_ {0}}}$${\ displaystyle W_ {t_ {1}}}$

Decomposição espectral

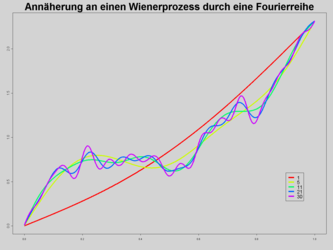
Com a decomposição espectral, o processo de Wiener é aproximado em uma espécie de análise estocástica de Fourier como polinômios trigonométricos com coeficientes aleatórios. Se eles são independentes e com distribuição normal padrão, a série converge${\ displaystyle Z_ {0}, \; Z_ {1}, \; Z_ {2} \ ldots}$

${\ displaystyle S (t) = Z_ {0} \ cdot t + \ sum _ {k = 1} ^ {\ infty} Z_ {k} ~ {\ frac {{\ sqrt {2}} \ cdot \ sin ( k \ pi t)} {k \ pi}}}$

contra um julgamento vienense. Este método converge com velocidade máxima em relação à norma L ² , mas ao contrário da ponte browniana, contém muitas avaliações complexas de funções trigonométricas. É por isso que é usado com menos frequência , especialmente na simulação de Monte Carlo .

• Abordagem de um processo Wiener por meio de uma série de Fourier
• 
• 

geometria

O movimento browniano unidimensional e bidimensional é recorrente , em todas as dimensões superiores é transitório . ( Frase de Pólya (passeios aleatórios) : "Um homem bêbado sempre encontra o caminho de casa, um pássaro bêbado não.")

Veja também

• Movimento browniano quebrado
• Processo de difusão de raiz

literatura

• Andrei N. Borodin, Paavo Salminen: Manual do movimento browniano - fatos e fórmulas. Birkhäuser, Basel 2002, ISBN 3-7643-6705-9 .
• Ioannis Karatzas, Steven E. Shreve: movimento browniano e cálculo estocástico (textos de graduação em matemática). Springer, New York 1997, ISBN 0-3879-7655-8 .
• David Meintrup, Stefan Schäffler: Stochastics. Teoria e aplicações. Springer, Berlin / Heidelberg 2005, ISBN 3-540-21676-6 , cap. 12, pp. 341-374.
• René L. Schilling, Lothar Partzsch: Brownian Motion. Uma introdução aos processos estocásticos. De Gruyter, Berlin / Boston 2012, ISBN 978-3-11-027889-7 .
• John Michael Steele: Cálculo Estocástico e Aplicações Financeiras. Springer, New York 2000, ISBN 0-387-95016-8 .

Evidência individual

1. ↑ Einstein, Albert: Sobre o movimento de partículas suspensas em líquidos em repouso, exigido pela teoria cinética molecular do calor. In: Annals of Physics . fita 17 , 1905, pp. 549-560 . 
2. ↑ Smoluchowski, M.: Sobre a teoria cinética do movimento molecular browniano e suspensões . In: Annals of Physics . fita 21 , 1906, pp. 756-780 . 
3. ↑ P. Lévy: Processus stochastiques et mouvement brownien. Gauthier-Villars, Paris 1965.