Modelo Black-Scholes

O modelo Black-Scholes (pronuncia-se ˌblæk ˈʃoʊlz ) é um modelo matemático financeiro para avaliação de opções financeiras , publicado por Fischer Black e Myron Samuel Scholes em 1973 (após ter sido rejeitado duas vezes por revistas renomadas) e é considerado um marco no setor financeiro .

história

Robert C. Merton também esteve envolvido na redação (além dos dois acima), mas publicou um artigo separado. Para ser justo, o modelo também deveria levar seu nome, mas isso nunca pegou. No entanto, Merton foi homenageado juntamente com Scholes pelo desenvolvimento deste modelo com o Prêmio do Reichsbank for Economics da Suécia em 1997 ; Fischer Black morreu em 1995. No entanto, Black também definiu acentos de avaliação diferentes de Scholes e Merton.

Moldura do modelo

A análise que leva ao modelo Black-Scholes olha para qualquer derivado que tenha uma ação não pagadora de dividendos como seu subjacente .

Suposições

O modelo original faz algumas suposições idealizadoras:

1. O preço do valor base , ou seja , o preço da ação , segue um movimento browniano geométrico com deriva e volatilidade constantes .
2. A venda a descoberto de instrumentos financeiros é possível sem restrições.
3. Não há custos de transação ou impostos. Todos os instrumentos financeiros podem ser negociados em qualquer unidade pequena.
4. Não há pagamento de dividendos sobre as ações subjacentes desde o momento em que o derivativo é fechado até a data de vencimento .
5. Não há opção livre de risco para arbitragem ( sem arbitragem ).
6. Os instrumentos financeiros são negociados continuamente.
7. Existe uma taxa de juros livre de risco que é constante ao longo do tempo e a mesma para todos os prazos.

Em extensões de modelo, pagamentos de dividendos, estocásticos taxas de juros ou estocásticos volatilidades também são considerados.

Modelo de Black-Scholes e equação diferencial de Black-Scholes

A ideia básica é construir uma carteira livre de risco a partir do derivativo e da ação. Nesse contexto, “livre de risco” significa que o valor da carteira por curtos períodos de tempo - sinônimo de pequenas variações no preço da ação - não depende do preço da ação.

De acordo com as premissas, o preço das ações se move de acordo com um movimento browniano geométrico com incremento e mudanças de preço incrementais${\ displaystyle S}$

${\ displaystyle \ mathrm {d} S = \ mu \, S \, \ mathrm {d} t + \ sigma \, S \, \ mathrm {d} W}$.

É o retorno esperado do preço da ação, a volatilidade e o tempo. denota um processo Wiener padrão . pode ser visto como um aumento infinitesimal no comprimento ao longo de um intervalo de tempo , ou seja, H. como uma variável aleatória normalmente distribuída com expectativa e variância . ${\ displaystyle \ mu}$${\ displaystyle \ sigma> 0}$${\ displaystyle t \ geq 0}$${\ displaystyle W}$${\ displaystyle \ mathrm {d} W}$${\ displaystyle W_ {t}}$${\ displaystyle \ mathrm {d} t}$${\ displaystyle 0}$${\ displaystyle \ mathrm {d} t}$

Com o lema de Itō obtém-se a fórmula para as mudanças no valor de uma derivada ${\ displaystyle V}$

${\ displaystyle \ mathrm {d} V = \ left ({\ frac {\ parcial V} {\ parcial t}} + \ mu \, S {\ frac {\ parcial V} {\ parcial S}} + {\ frac {1} {2}} \, \ sigma ^ {2} \, S ^ {2} \, {\ frac {\ partial ^ {2} V} {\ partial S ^ {2}}} \ right) \ mathrm {d} t + \ sigma \, S \, {\ frac {\ parcial V} {\ parcial S}} \, \ mathrm {d} W}$.

Aqui e estão os mesmos valores de antes, já que o preço do derivado depende do processo de precificação da ação. ${\ displaystyle \ mu}$${\ displaystyle W}$

O processo de Wiener, portanto, influencia o preço da ação por meio de um fator e o valor do derivado por meio de um fator . A carteira, que é isenta de risco em termos de análise, consiste, portanto, em ${\ displaystyle W}$${\ displaystyle \ sigma \, S}$${\ displaystyle \ sigma \, S \, {\ frac {\ parcial V} {\ parcial S}}}$

• -1 derivados ( ou seja, uma posição curta no derivado)
• ${\ displaystyle {\ frac {\ partial V} {\ partial S}}}$ Pedaços de estoque

(Ou com o sinal oposto: uma posição comprada no derivado e uma posição vendida nas ações do tamanho especificado). Na prática, este conceito de cobertura de carteira é utilizado na forma de cobertura delta .

Com os pesos de carteira dados e os processos de preços para ações e derivativos, o valor da carteira e as mudanças no valor da carteira podem ser formulados em curtos períodos de tempo.

O valor do portfólio é ${\ displaystyle \ P}$

${\ displaystyle P = -V + S \, {\ frac {\ parcial V} {\ parcial S}}}$,

ou seja, a soma do valor negativo do derivado mais o valor das ações. A mudança no valor da carteira em curtos períodos de tempo pode ser escrita como ${\ displaystyle {\ frac {\ partial V} {\ partial S}}}$${\ displaystyle \ mathrm {d} P}$

${\ displaystyle \ mathrm {d} P = - \ mathrm {d} V + \ mathrm {d} S \, {\ frac {\ partial V} {\ partial S}} = \ left (- {\ frac {\ parcial V} {\ parcial t}} - {\ frac {1} {2}} \, \ sigma ^ {2} \, S ^ {2} \, {\ frac {\ parcial ^ {2} V} { \ parcial S ^ {2}}} \ direita) \ mathrm {d} t}$.

As mudanças de preço na carteira, portanto, não dependem das mudanças aleatórias de preço no preço das ações do Teste de Viena, nem do retorno esperado da ação . O segundo ponto é uma lição importante do modelo Black-Scholes. ${\ displaystyle W}$${\ displaystyle \ mu}$

Uma vez que a carteira é livre de risco e, de acordo com as premissas, não há oportunidades de arbitragem, a carteira deve gerar precisamente o retorno livre de risco em curtos períodos de tempo , ou seja, ${\ displaystyle r}$

${\ displaystyle \ mathrm {d} P = r \, P \, \ mathrm {d} t}$

Substituir isso na última equação dá a equação diferencial de Black-Scholes

${\ displaystyle {\ frac {\ parcial V} {\ parcial t}} + r \, S {\ frac {\ parcial V} {\ parcial S}} + {\ frac {1} {2}} \, \ sigma ^ {2} \, S ^ {2} \, {\ frac {\ parcial ^ {2} V} {\ parcial S ^ {2}}} = r \, V}$.

De acordo com os pressupostos dados, esta equação é válida para todos os derivados que podem ser definidos com base no processo de precificação para O tipo de derivada para a qual a equação deve ser resolvida determina as condições de contorno para a equação diferencial. ${\ displaystyle S}$

Musiela e Rutkowski, em particular, apontaram que o portfólio usado para derivar a equação diferencial de Black-Scholes não é autofinanciável. O raciocínio é intuitivo e fornece a equação diferencial de Black-Scholes. De um ponto de vista matemático financeiro, entretanto, a derivação é problemática. Musiela e Rutkowski também fornecem uma derivação financeiramente convincente.

Preços de opções Black-Scholes

As opções europeias fornecem os fluxos de capital no final do prazo (em ) ${\ displaystyle t = T}$

${\ displaystyle {\ mathit {CF _ {\ text {call}}}} (T) = \ max \ {SK; 0 \}}$ para uma chamada

respectivamente

${\ displaystyle {\ mathit {CF _ {\ text {put}}}} (T) = \ max \ {KS; 0 \}}$ para uma colocação

O preço justo da opção pode ser derivado de vários argumentos. Pode ser mostrado como o valor esperado descontado dos pagamentos mencionados em , sendo que o valor esperado deve ser formado em relação à medida neutra ao risco. Outra forma de derivar uma fórmula explícita para os preços das opções é resolver a equação diferencial de Black-Scholes, na qual os pagamentos nos vencimentos são considerados como condições de contorno. ${\ displaystyle T}$

Fórmulas de preços

A fórmula de preço Black-Scholes para uma opção de compra ou venda na Europa é obtida das duas maneiras:

${\ displaystyle C (S, t) = S \ Phi (d_ {1}) - Ke ^ {- r (Tt)} \ Phi (d_ {2})}$

respectivamente

${\ displaystyle P (S, t) = Ke ^ {- r (Tt)} \ Phi (-d_ {2}) - S \ Phi (-d_ {1})}$

no qual

${\ displaystyle d_ {1} = {\ frac {\ ln (S / K) + (r + \ sigma ^ {2} / 2) (Tt)} {\ sigma {\ sqrt {Tt}}}}}$

${\ displaystyle d_ {2} = {\ frac {\ ln (S / K) + (r- \ sigma ^ {2} / 2) (Tt)} {\ sigma {\ sqrt {Tt}}}} = d_ {1} - \ sigma {\ sqrt {Tt}}}$

${\ displaystyle \ Phi (x) = \ int _ {- \ infty} ^ {x} {\ frac {1} {\ sqrt {2 \ pi}}} \ exp {\ Bigl (} - {\ frac {ex .: ^ {2}} {2}} {\ Bigr)} \, \ mathrm {d} z}$ indica a função de distribuição do padrão normal de distribuição .

O valor de uma opção é, portanto, determinado por 5 parâmetros:

• ${\ displaystyle S}$: preço atual da ação
• ${\ displaystyle r}$: taxa de juros congruente com o prazo remanescente da opção
• ${\ displaystyle \ sigma}$: A volatilidade futura do subjacente. Esta é a única variável desconhecida quando o contrato é celebrado e, portanto, em última análise, é objeto de preços entre as partes contratantes.
• ${\ displaystyle Tt}$: Prazo remanescente da opção com prazo total na época${\ displaystyle T}$${\ displaystyle t}$
• ${\ displaystyle K}$: Preço base, definido como parte do contrato

Os gregos de acordo com Black-Scholes

Como gregos ( Inglês gregos ) são chamados as derivadas parciais do preço da opção de acordo com os respectivos parâmetros do modelo. A vantagem da fórmula explícita para os preços das opções - ao contrário de uma solução numérica , por exemplo - é que esses derivados podem ser facilmente calculados.

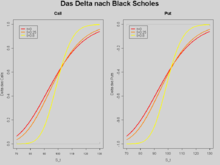
delta

Delta de uma opção europeia depois de Black e Scholes

Delta de uma chamada ao longo do tempo; cada um de, em e no dinheiro. O curso é exatamente o mesmo para a tacada, apenas deslocado para baixo

O delta indica em quanto o preço da opção muda se o preço do subjacente muda em uma unidade e todos os outros fatores de influência permanecem os mesmos. Por exemplo, uma opção de compra (call) "deep in the money" tem um delta de +1 e uma opção de venda "deep in the money" (-1).

No modelo Black-Scholes, o delta é calculado como:

${\ displaystyle \ Delta _ {c} = {\ frac {\ parcial C} {\ parcial S}} = \ Phi (d_ {1}) \ geq 0}$

para a chamada europeia, resp.

${\ displaystyle \ Delta _ {p} = {\ frac {\ parcial P} {\ parcial S}} = - \ Phi (-d_ {1}) = \ Phi (d_ {1}) - 1 \ leq 0}$

para a colocação.

gama

O gama é a segunda derivada do preço da opção após o preço do ativo subjacente. É o mesmo para ligar e colocar no modelo Black-Scholes

${\ displaystyle \ Gamma = {\ frac {\ partial ^ {2} C} {\ partial S ^ {2}}} = {\ frac {\ varphi (d_ {1})} {S \ sigma {\ sqrt { Tt}}}} = {\ frac {\ Phi '(d_ {1})} {S \ sigma {\ sqrt {Tt}}}} \ geq 0}$.

Logo, o gama não é negativo, ou seja, o preço da opção muda sempre na mesma direção (alta / queda) da volatilidade. Se a opção estiver no dinheiro (inglês no dinheiro ), a gama com vencimento decrescente pode aumentar além de todos os limites. A carta representa a função densidade da distribuição normal , consulte função de distribuição . ${\ displaystyle \ mathrm {\ varphi}}$${\ displaystyle \ Phi}$

Gama de uma opção europeia segundo Black e Scholes

Vega (Lambda, Kappa)

Vega, também chamado de lambda ou kappa, descreve a derivação do preço da opção de acordo com a volatilidade e, portanto, indica a força com que uma opção reage a mudanças na volatilidade (constante no modelo Black-Scholes). O Vega é o mesmo para uma chamada e colocação europeias, nomeadamente

${\ displaystyle \ Lambda = {\ frac {\ parcial C} {\ parcial \ sigma}} = {\ frac {\ parcial P} {\ parcial \ sigma}} = S \ varphi (d_ {1}) {\ sqrt {Tt}} = S \ Phi '(d_ {1}) {\ sqrt {Tt}} \ geq 0}$.

Vega não é uma letra grega . Sigma já está atribuído como um símbolo para o desvio padrão . A volatilidade é usada como uma estimativa do desvio padrão futuro.

Theta

O teta denota a derivada de acordo com o tempo decorrido t, ou seja, indica a sensibilidade da opção a mudanças no tempo. Uma vez que, todas as coisas sendo iguais , o valor de uma opção se aproxima do pagamento na data de vencimento ao longo do tempo, o teta de uma opção de compra europeia nunca é positivo e a opção perde valor com o tempo. Também é conhecido como valor de tempo da opção. No modelo Black-Scholes é

${\ displaystyle \ Theta _ {c} = {\ frac {\ parcial C} {\ parcial t}} = - {\ frac {S \ varphi (d_ {1}) \ sigma} {2 {\ sqrt {Tt} }}} - rKe ^ {- r (Tt)} \ Phi (d_ {2})}$

ou.

${\ displaystyle \ Theta _ {p} = {\ frac {\ parcial P} {\ parcial t}} = - {\ frac {S \ varphi (d_ {1}) \ sigma} {2 {\ sqrt {Tt} }}} + rKe ^ {- r (Tt)} \ Phi (-d_ {2})}$.

Rho

Rho descreve a sensibilidade da opção a pequenas mudanças na taxa de juros.

${\ displaystyle \ mathrm {P} _ {c} = {\ frac {\ parcial C} {\ parcial r}} = (Tt) Ke ^ {- r (Tt)} \ Phi (d_ {2}) \ geq 0}$

${\ displaystyle \ mathrm {P} _ {p} = {\ frac {\ parcial P} {\ parcial r}} = - (Tt) Ke ^ {- r (Tt)} \ Phi (-d_ {2}) \ leq 0}$.

ómega

A elasticidade da opção é uma sensibilidade percentual:

${\ displaystyle \ Omega _ {c} = {\ frac {\ frac {\ Delta C} {C}} {\ frac {\ Delta S} {S}}} = \ Phi (d_ {1}) {\ frac {S} {C}}> 0}$

${\ displaystyle \ Omega _ {p} = {\ frac {\ frac {\ Delta P} {P}} {\ frac {\ Delta S} {S}}} = (\ Phi (d_ {1}) - 1 ) {\ frac {S} {P}} <0}$.

usar

Os gregos são importantes para a gestão de riscos. Eles facilitam a análise da influência dos fatores de risco individuais. Isto é particularmente verdadeiro ao nível de uma carteira de instrumentos financeiros, quando se pretende estimar a influência de fatores de risco individuais - nomeadamente os parâmetros do modelo - na carteira global. Um exemplo seria um portfólio de opções e posições no subjacente associado, por ex. B. Opções sobre as posições de Futuro do Euro Bund e Futuro do Euro Bund como tal. O efeito (linear) de uma mudança no preço futuro sobre a carteira geral pode ser exibido usando o delta.

É por isso que os gregos também podem ser usados ​​como proteção contra riscos . O exemplo mais conhecido é o delta hedging . A sensibilidade Rho pode ser usada, por exemplo, para determinar como uma carteira de opções deve ser protegida contra mudanças na taxa de juros de refinanciamento.

Preços de uma ligação Black Scholes

Os gráficos à direita mostram as curvas com os valores das chamadas europeias com diferentes termos restantes. Estes não se sobrepõem e quanto mais alto, mais longo será o prazo restante. A curva mais baixa e distorcida é o valor intrínseco da opção, dependendo da taxa base atual hoje.

1. Os valores das opções aumentam monotonamente (não tem de ser o caso em geral, como é o caso das opções de taxa de juro ).
2. O preço da opção de compra europeia é sempre superior ao seu valor intrínseco. Em termos econômicos, isso significa que é sempre melhor vender a opção de compra no mercado do que antes, pois o valor intrínseco (hoje) é menor que o preço de venda no mercado. Isso se torna relevante no caso das ligações americanas, pois estas têm direito de exercício antecipado. Como regra geral, o exercício antecipado de opções americanas não tem valor enquanto se tratar de um bem sem rentabilidade (sem dividendo dentro do período da opção).
3. Sensibilidade em relação ao preço do ativo-objeto: Delta : A inclinação da tangente à curva do valor da opção corresponde ao delta do modelo binomial .
   1. am Geld ( ): O delta é aproximadamente 1/2. Quanto maior for o preço da ação, maior será a inclinação, o delta.${\ displaystyle S = E}$${\ displaystyle S_ {0}}$
   2. fundo no dinheiro : o valor da opção reage como o próprio preço da ação.
4. Sensibilidade do delta em relação ao preço da opção: Gama : Gama é a curvatura da curva, a convexidade (matemática: segunda derivada do valor da opção de compra de acordo com o preço da ação)
   1. longe do dinheiro : gama está perto de zero, i. H. o delta permanece constante.
   2. no fundo do dinheiro : gama é próxima de zero.
5. Sensibilidade em relação ao termo: Theta : Mudança no valor da opção no decorrer do tempo do calendário. Pouco antes da data de vencimento, o valor da chamada é extremamente sensível ao tempo e possui alta convexidade.
   1. longe do dinheiro : grande perda de posição
   2. no dinheiro : perda média
   3. fundo no dinheiro : grande lucro

fraquezas

No modelo de Black-Scholes, a volatilidade σ é considerada constante. No entanto, todos os cálculos ex-post dos desvios padrão dos retornos mostram que a volatilidade não é constante ao longo do tempo. Outra fraqueza é que a volatilidade, a variável mais importante, deve ser prevista por si mesmo. Isso é feito com a ajuda de modelos de regressão extrapolando valores passados ​​ou determinando as volatilidades implícitas (veja lá) que podem ser baseadas nos preços de mercado atuais. Além disso, o modelo contém a suposição simplificadora de que os retornos são normalmente distribuídos . A distribuição normal tem pouco peso em suas extremidades, o que significa que muito pouca consideração pode ser levada em consideração a ocorrência de eventos extremos (ver curvatura (estatísticas) ). Essas limitações do modelo Black-Scholes podem ser vistas nos preços negociados das opções quando se considera as volatilidades implícitas nos preços das opções . A volatilidade implícita de uma opção sobre um determinado objeto não é constante, mas muda com o tempo. Além disso, a volatilidade implícita para um determinado momento depende da proximidade do dinheiro ("moneyness", veja também o sorriso da volatilidade ) e do prazo remanescente da opção (estrutura temporal da volatilidade). Ambas as observações não concordam com a suposição do modelo de uma volatilidade uniforme e constante. O uso de volatilidades implícitas que dependem do vencimento remanescente e da moeda são um método de lidar com as limitações do modelo Black-Scholes. Se outro modelo se tornasse padrão no mercado de opções, em vez da fórmula de preço de Black-Scholes, pode-se supor que não seriam os preços das opções negociadas, mas as volatilidades implícitas no modelo que mudariam.

Modelos avançados em que a volatilidade é considerada uma função decrescente do preço das ações, como B. o modelo CEV, dá melhores resultados.

Derivação

O modelo Black-Scholes pode ser interpretado como um caso limite do modelo binomial discreto de tempo e valor de acordo com Cox, Ross e Rubinstein, em que os intervalos de negociação são definidos cada vez mais curtos:

${\ displaystyle \ Delta t \ to 0}$.

${\ displaystyle u (\ Delta t)}$e perder peso de forma controlada. Os retornos do preço das ações no modelo discreto são distribuídos binomialmente. Eles convergem para uma distribuição normal. Os preços das ações são, então, logaritmicamente distribuídos normalmente em cada momento. Normalmente, um número de etapas de 100 é suficiente com a restrição de opções exóticas ou sensibilidades de opção. ${\ displaystyle d (\ Delta t)}$

literatura

Trabalho original

• Fischer Black , Myron Scholes : O preço de opções e responsabilidades corporativas. In: Journal of Political Economy. 81, 3, 1973, ISSN  0022-3808 , pp. 637-654.
• Robert C. Merton : Teoria da Precificação de Opções Racionais. In: The Bell Journal of Economics and Management Science. 4, 1973, ISSN  0005-8556 , pp. 141-183.

Crítica teórica

• Nasser Saber: Speculative Capital. Financial Times et al., Londres 1999
  • Vol. 1: A mão invisível das finanças globais. ISBN 0-273-64155-7 ,
  • Vol. 2: A natureza do risco nos mercados de capitais. ISBN 0-273-64422-X .

Links da web

• Palestras do Nobel de 1997 por Scholes e Merton
• American Mathematical Society ( Memento de 20 de abril de 2005 no Internet Archive ) para o Prêmio Nobel de Economia 97, com outros links
• Teoria e calculadora online (incluindo VAR e os gregos) do modelo de opção Black-Scholes por Jan-Hendrik Dörner, Universidade Goethe, Frankfurt am Main.
• Apresentação informal de várias páginas da Bradley University com extensa bibliografia
• Macros do Excel para calcular o preço da opção
• Simulador de hedge Mostra o resultado de um hedge delta e delta-gama (replicação) em tempo discreto em um modelo de Black-Scholes.
• Calculadora online (incluindo gregos e código-fonte para download) do modelo de opção Black-Scholes

Evidência individual

1. ^ Pronúncia correta de Black-Scholes em Merriam-Webster
2. ↑ Mehrling, Perry : "Understanding Fischer Black" primeiro rascunho dos capítulos do livro que tratam dos anos acadêmicos de Black "Fischer Black e a ideia revolucionária das finanças" ( Memento de 22 de junho de 2010 no Internet Archive ) (PDF; 158 kB), 2005
3. ↑ Representação de acordo com: John C. Hull: Opções, futuros e outros derivativos. 9ª ed., Pearson Education, 2015, ISBN 978-0-13-345631-8 , p. 331.
4. ↑ A derivação nesta seção segue: John C. Hull: Opções, futuros e outros derivativos. 9ª edição, Pearson Education, 2015, ISBN 978-0-13-345631-8 , pp. 331 e segs.
5. ^ Marek Musiela, Marek Rutkowski: Martingale Methods in Financial Modeling . 2ª Edição. Springer, Berlin / Heidelberg 2005, p. 107 . 
6. ^ Marek Musiela e Marek Rutkowski: Martingale Methods in Financial Mathematics . 2ª Edição. Springer, Berlin / Heidelberg, p. 96 ff . 
7. ↑ Igor Uszczapowski: Noções básicas sobre opções e futuros. Noções básicas e novos desenvolvimentos. 6ª edição atualizada e ampliada. Deutscher Taschenbuchverlag, Munich 2008, ISBN 978-3-423-05808-7 ( alemão. 5808. Beck-Wirtschaftsberater ).
8. ^ John C. Hull : Opções, futuros e outros derivados. 3ª edição. Prentice Hall International, Upper Saddle River NJ 1997, ISBN 0-13-264367-7 , pp. 503-505, 510f ( Prentice-Hall International Editions ).