Método do elemento finito

Visualização de uma simulação FEM da deformação de um carro em uma colisão frontal assimétrica

Representação da distribuição de calor em uma carcaça de bomba com o auxílio da equação de condução de calor . Os “elementos finitos” podem ser vistos com as arestas dos elementos como linhas pretas.

O método dos elementos finitos (FEM), também conhecido como " método dos elementos finitos ", é um método numérico geral usado para várias tarefas físicas . O mais conhecido é a aplicação do FEM na análise de resistência e deformação de sólidos com formas geometricamente complexas, pois aqui o uso de métodos clássicos (por exemplo, a teoria do feixe ) se mostra muito demorado ou impossível. Logicamente, o FEM é baseado na solução numérica de um complexo sistema de equações diferenciais .

O domínio computacional (por exemplo. Como os sólidos) é mais fácil em um número finito de sub-regiões (z. B. corpo parcial) forma dividida tal. B. em muitos cubóides pequenos ou tetraedros . Eles são os "elementos finitos". Devido à sua geometria simples, seu comportamento físico pode ser bem calculado com funções de forma conhecidas . O comportamento físico de todo o corpo é simulado pela forma como esses elementos reagem às forças, cargas e condições de contorno e como cargas e reações são propagadas durante a transição de um elemento para o próximo devido a condições de continuidade dependentes do problema muito específicas que a abordagem funções devem cumprir.

As funções de abordagem contêm parâmetros que geralmente têm um significado físico, como B. o deslocamento de um determinado ponto no componente em um determinado ponto no tempo. A busca pela função de movimento é assim reduzida à busca dos valores dos parâmetros das funções. A precisão da solução aproximada pode ser melhorada usando mais e mais parâmetros (por exemplo, mais e mais, elementos menores) ou mais e mais funções de abordagem valiosas.

O desenvolvimento do FEM só foi possível em etapas essenciais por meio do desenvolvimento de poderosos computadores, pois requer considerável poder computacional. Portanto, este método foi formulado de maneira amigável ao computador desde o início. Trouxe um avanço significativo no tratamento de áreas computacionais de qualquer formato.

introdução

Modelo estrutural gerado de um pistão alternativo (motor diesel) como um componente de um motor de combustão interna para fins de análise de tensão

Com o FEM, problemas de diferentes disciplinas físicas podem ser calculados, pois é basicamente um método numérico para resolver equações diferenciais . Primeiro, a área de cálculo (“componente”) é dividida em um grande número de elementos - suficientemente finos. Esses elementos são finitamente pequenos, mas seu tamanho real permanece matematicamente relevante - eles não são "infinitamente pequenos" (infinitos). A divisão da área / componente em um certo número de elementos de tamanho finito, que podem ser descritos com um número finito de parâmetros, deu ao método o nome de "método dos elementos finitos".

Existem funções de forma para esses elementos (por exemplo, abordagens Ritz locais por elemento) que descrevem como um elemento reage a influências externas e condições de limite. Se você inserir essas funções de forma para todos os elementos nas equações diferenciais a serem resolvidas, que descrevem as leis físicas, obterá um sistema de equações muito grande junto com as condições iniciais, de contorno e de transição. Resolvê-lo (pelo menos aproximadamente) é a tarefa do solucionador de equações FE. O tamanho do sistema de equações a ser resolvido depende muito do número de elementos finitos. Sua solução aproximada representa, em última análise, a solução numérica da equação diferencial em consideração; Se foi resolvido para todos os elementos como eles se comportam sob as cargas, então isso também resulta na reação de todo o componente.

Finito, infinito

Matematicamente, o tamanho de cada elemento permanece relevante e também deve ser incluído em seu cálculo, ele é apenas "finitamente" pequeno. No caso de elementos 'infinitamente' pequenos, seu tamanho seria desprezível e não seria mais levado em consideração nas equações. Nesse sentido, o tamanho do elemento permanece relevante.

Uma divisão “suficientemente fina” do componente em elementos está presente se o refinamento posterior não tiver mais qualquer influência significativa no resultado do cálculo. I. E. o resultado geral é independente do tamanho do elemento, que (desse ponto de vista) não é mais relevante. Se o tamanho do elemento ainda tiver um impacto significativo no resultado geral, então i se aplica. A. a malha não está boa o suficiente.

história

O uso do FEM na prática começou na década de 1950 com um cálculo estrutural de asas de aeronaves na indústria aeroespacial ( Turner , Clough 1956) e muito em breve também na construção de veículos. O método é baseado no trabalho da Daimler AG em Stuttgart, que usou o programa FEM desenvolvido por si mesmo, ESEM (Elastostatic Element Method), muito antes do design auxiliado por computador (CAD) ser introduzido no início dos anos 1980. O termo método dos elementos finitos foi proposto pela primeira vez por RW Clough em 1960 e tem sido usado em todos os lugares desde os anos 1970. O termo mais comum em alemão para usuários industriais é engenheiro de cálculo .

A história do método dos elementos finitos emerge das pesquisas e publicações dos seguintes autores (seleção):

• Karl Heinrich Schellbach : cálculo das variações ; Solução de um problema de área mínima (1851/52)
• Ernst Gustav Kirsch: As equações fundamentais da teoria da elasticidade dos corpos sólidos, derivadas da consideração de um sistema de pontos que são conectados por escoras elásticas (1868)
• John William Strutt, 3º Barão Rayleigh (1842-1919): Sobre a teoria da ressonância. 1870
• Walter Ritz (1878-1909): novo método para resolver problemas de variação, método de Ritz (1908/09)
• Boris G. Galerkin (1871-1945): Método de resíduos ponderados (1915)
• Erich Trefftz (1926): funções de abordagem limitadas localmente; Contraparte ao método Ritz
• Hans Ebner (1929): Schubblech como um elemento de nível na construção de aeronaves
• Alexander Hrennikoff (1896–1984): modelos de haste, substituição de painéis por armações, painéis com grades de suporte 1940/41
• Richard Courant (1888–1972): Métodos variacionais para a solução de problemas de equilíbrio e vibração (ões). 1943 (funções de abordagem com suporte local, abordagens por elemento para problemas de vibração)
• William Prager (1903–1980), John Lighton Synge (1897–1995): Aproximação na elasticidade com base no conceito de espaço funcional. 1947
• John Argyris (1913-2004): Método de força e deslocamento para estruturas de barra, formulação de matriz (1954/55)
• MJ Turner, Ray W. Clough , HC Martin, LJ Topp: Análise de rigidez e deflexão de estruturas complexas. 1956 (primeiro cálculo estrutural de asas de aeronaves na Boeing , primeira aplicação de FEM com programa de computador, primeira aplicação de elementos de superfície)
• Ray W. Clough (1920-2016): O método dos elementos finitos na análise de tensões planas. 1960 (provavelmente o primeiro uso do termo elementos finitos)
• Spierig (1963): Desenvolvimento de elementos triangulares, transferência para conchas
• Olgierd Cecil Zienkiewicz (1921–2009), pioneiro do FEM e primeiro trabalho padrão (livro didático): O Método dos Elementos Finitos em Mecânica Estrutural e Contínua , 1967 (com YK Cheung)
• Alfred Zimmer (* 1920) e Peter Groth (* 1938), pioneiros do FEM, primeiro livro-texto alemão do FEM: Element Method of Elastostatics , 1969 Oldenbourg Verlag Munich, Vienna
• Olga Alexandrovna Ladyschenskaja (1922–2004), Ivo Babuška (* 1926) e Franco Brezzi (* 1945) - Condição Ladyschenskaja-Babuška-Brezzi para a estabilidade de um problema de elemento finito misto com uma estrutura de ponta de sela
• Ivo Babuška (* 1926) - algoritmos de elementos finitos adaptativos

aplicativo

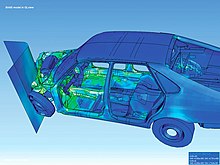
A primeira aplicação do FEM foi o tratamento linear de sólidos e estruturas na forma do método de deslocamento e a partir disso o FEM recebeu seus impulsos. O termo “elementos finitos” foi usado um pouco mais tarde. No curso posterior da pesquisa, o método dos elementos finitos foi generalizado cada vez mais e agora pode ser usado em muitos problemas físicos, incluindo pode ser usado em vários cálculos de campo acoplados, previsões do tempo ou para questões técnicas nas indústrias automotiva, médica, aeroespacial, mecânica ou de bens de consumo na engenharia. Uma das principais áreas de aplicação do método é o desenvolvimento de produtos , por meio do qual, entre outras coisas, cálculos de resistência mecânica de componentes individuais ou, por exemplo, chassis completos e estruturas de carroceria são calculados para economizar tempo em testes de colisão .

Procedimento para um cálculo mecânico linear (exemplar)

Os programas que usam o método dos elementos finitos funcionam de acordo com o princípio EVA : O usuário cria uma geometria (componente) em um programa CAD. Ele então faz outras entradas no chamado pré - processador FE . Um solucionador de equações FEM realiza o cálculo real e o usuário recebe os resultados calculados, que podem então ver no chamado pós - processador FE na forma de exibições gráficas. Freqüentemente, o pré-processador e o pós-processador são combinados em um programa ou mesmo fazem parte do programa CAD.

Cálculo da força linear da cadeia de processo

Entrada: pré-processador

O componente é projetado no programa CAD e transferido para o pré-processador FE usando uma interface direta ou um formato de troca neutro como o STEP . Ao selecionar parâmetros de rede, como tamanho e tipo de elemento (por exemplo, tetraedro, hexaedro em 3D) no módulo de malha, os elementos finitos são gerados com a ajuda de um algoritmo de malha. Para a análise de resistência mecânica, o comportamento do material deve ser inserido, o que indica essencialmente quais reações o componente tem para cargas externas (por exemplo, deformação). Dependendo do material, a relação entre tensão e deformação é diferente e existem diferentes deformações. Se esta relação for linear, apenas o módulo de elasticidade e o coeficiente de Poisson são necessários para o cálculo de FE , caso contrário, outros parâmetros de material e entradas no pré-processador são necessários. Outras condições de contorno são, por exemplo, cargas atuando no componente (forças, pressão, temperatura, etc.). Para obter uma representação o mais realista possível, são especificadas as condições de contorno homogêneas (restrições) e não homogêneas (deslocamentos), bem como todas as cargas a serem consideradas no modelo.

Processamento: solucionador de equações

Dependendo do programa, um solucionador de equações separado (programa autônomo) ou integrado é usado. Ele calcula a simulação de como as cargas, forças e condições de contorno afetam os elementos individuais do componente e como as forças e os efeitos se propagam no componente e afetam os elementos vizinhos. O cálculo primeiro fornece uma solução aproximada grosseira. Outras iterações melhoram a aproximação. A maioria das iterações é calculada até que haja apenas as menores alterações - então a aproximação "convergiu" e é o resultado da simulação.

Saída: pós-processador

No caso do cálculo de resistência mecânica, o usuário recebe o resultado do solucionador de equações FEM em valores específicos de tensão , deformação e alongamento . O pós-processador pode exibir isso em uma imagem de cor falsa , por exemplo . Os valores de tensão equivalente são usados, por exemplo, para verificar a resistência de um componente.

Funcionalidade geral

Discretização

O método dos elementos finitos é um método discreto; H. a solução é calculada em um subconjunto discreto da área de base. Para este propósito, ele é dividido em subáreas simples, os chamados elementos finitos (rede, malha). O termo “finito” enfatiza a diferença para a consideração analítica de elementos infinitesimais. Os cantos dos elementos finitos são chamados de nós. Esses nós formam o subconjunto discreto do método numérico. As funções de aproximação são introduzidas nos elementos, que contêm os tamanhos de nós desconhecidos como parâmetros. As aproximações locais são introduzidas na formulação fraca do problema do valor de contorno. Os integrais do elemento resultante são calculados com quadratura numérica. As abordagens de aproximação são "integradas" para que apenas os valores dos nós permaneçam nos elementos como desconhecidos após a integração. As equações do elemento são montadas por meio de requisitos de continuidade nos limites do elemento. Desta forma, os problemas de valor limite para equações diferenciais parciais lineares são convertidos em um sistema linear de equações com matrizes de sistema simétrico. Para equações diferenciais não lineares, o algoritmo é executado de forma análoga com a diferença de que as dependências não lineares são linearizadas iterativamente com métodos adequados (por exemplo, o método de Newton) e o sistema linear de equações é configurado para quantidades incrementais em cada subetapa.

Exemplo do uso de uma grade adaptativa para calcular o fluxo de ar em torno de uma asa de aeronave.

Para certas tarefas, a subdivisão em elementos é amplamente predeterminada pelo problema, por exemplo, no caso de estruturas espaciais nas quais as hastes individuais formam os elementos da construção. Isso também se aplica a construções de quadro, onde as vigas individuais ou peças de vigas subdivididas representam os elementos da tarefa. No caso de problemas bidimensionais, a área básica é dividida em triângulos ou quadrados. Mesmo se apenas elementos retos forem usados, uma aproximação muito boa da área básica pode ser obtida com uma discretização correspondentemente fina . Elementos curvilíneos aumentam a qualidade da aproximação. Em qualquer caso, esta discretização permite um registro flexível da área básica que também se adapta ao problema. No entanto, deve-se ter cuidado para evitar ângulos muito agudos ou obtusos nos nós de canto do elemento, a fim de excluir dificuldades numéricas. Em seguida, a área fornecida é substituída pela área dos elementos de aproximação. O teste de patch pode ser usado posteriormente para verificar se funcionou bem.

Os problemas espaciais são resolvidos com uma subdivisão da área tridimensional em elementos tetraédricos , elementos cubóides ou outros elementos adaptados ao problema, possivelmente também com arestas curvas, estes são i. d. Elementos de R. Serendipity ou Lagrange , editados.

A sutileza da subdivisão, i. H. a densidade da rede tem uma influência decisiva na precisão dos resultados do cálculo de aproximação. Uma vez que o esforço de computação aumenta ao usar redes mais finas e densas, é importante desenvolver soluções de rede que sejam o mais inteligentes possível .

Abordagem de elemento

Em cada um dos elementos, uma abordagem orientada para o problema é escolhida para a função procurada, ou mais geralmente para as funções que descrevem o problema. Funções racionais inteiras nas coordenadas espaciais independentes são particularmente adequadas para isso. Para elementos unidimensionais (membros, vigas), polinômios de primeiro, segundo, terceiro e, ocasionalmente, graus ainda mais elevados são questionados. No caso de problemas bidimensionais, são usados ​​polinômios lineares, quadráticos ou de ordem superior. O tipo de abordagem depende, por um lado, da forma do elemento e, por outro lado, o problema a ser tratado também pode influenciar a abordagem a ser escolhida. Porque as funções de abordagem devem atender a condições de continuidade dependentes do problema muito específicas na transição de um elemento para o próximo . Os requisitos de continuidade são frequentemente óbvios por razões físicas e também necessários por razões matemáticas. Por exemplo, o deslocamento de um corpo coerente em uma direção deve ser contínuo ao passar de um elemento a outro, a fim de garantir a continuidade do material. No caso de uma curva de viga ou placa, os requisitos de continuidade são maiores porque, por razões físicas análogas, a continuidade da primeira derivada ou das duas primeiras derivadas parciais deve ser exigida. Elementos com funções de forma que satisfazem as condições de continuidade são chamados de conformes.

Para realmente atender aos requisitos de continuidade, a curva de função no elemento deve ser expressa por valores de função e também por valores de derivadas ( parciais) (os deslocamentos do ponto nodal) em certos pontos do elemento, os pontos nodais . Os valores de função e valores de derivados usados ​​nos nós são chamados de variáveis ​​de nó do elemento. Com a ajuda dessas variáveis ​​de nó, a função de abordagem é representada como uma combinação linear das chamadas funções de forma com as variáveis ​​de nó como coeficientes.

É aconselhável usar um sistema de coordenadas global para as coordenadas do nó, além de um local relacionado ao elemento. Ambos estão ligados por funções de transformação. Se as mesmas funções de forma são usadas para esta transformação como para a abordagem de deformação, então eles são elementos isoparamétricos , para funções de elementos subparamétricos ou superparamétricos de grau inferior ou superior.

condições de fronteira

Após um dado problema ter sido discretizado e as matrizes de elementos configuradas, as condições de contorno são introduzidas . Um problema FE típico pode ter dois tipos de condições de contorno: condições de contorno de Dirichlet e condições de contorno de Neumann . Eles sempre se aplicam (funcionam) nos nós.

Uma condição de contorno de Dirichlet especifica diretamente um valor de função e uma condição de contorno de Neumann especifica uma derivada de um valor de função. Se uma condição de contorno de Dirichlet for fornecida, isso significa que o problema obtém um grau de liberdade a menos e a linha e coluna associadas na matriz geral são excluídas. Se a condição de contorno de Dirichlet não for igual a zero, o valor é adicionado à forma linear ("lado direito") de acordo com seu prefator. Dependendo do tipo de problema físico, diferentes quantidades físicas podem estar envolvidas, conforme mostrado a título de exemplo na tabela. As condições de contorno de Neumann também têm uma participação na forma linear (“lado direito”).

Uma outra variante são as condições de contorno periódicas , nas quais os valores em uma borda são tomados como dados para outra borda e, assim, uma área contínua periodicamente infinita é simulada. As chamadas condições de contorno cíclicas são definidas para problemas rotacionalmente simétricos .

Equações básicas do método de deslocamento

O método de deslocamento é a formulação padrão do método dos elementos finitos, em que os deslocamentos são as incógnitas primárias que descrevem a translação, rotação e deformação de um sólido. O método de deslocamento está disponível em todos os programas comuns de elementos finitos com os quais problemas em mecânica de sólidos podem ser calculados. Existem várias equações básicas para resolver problemas de estado sólido .

Princípio de d'Alembert na versão Lagrangiana

Uma das equações subjacentes ao método do deslocamento, com o qual os problemas gerais da mecânica dos sólidos podem ser tratados, é o princípio de d'Alembert , conforme formulado na descrição Lagrangiana da mecânica do contínuo . Com este princípio, tanto problemas lineares, como a questão das vibrações naturais, quanto problemas altamente não lineares, como testes de colisão , podem ser analisados. O método de resíduos ponderados de acordo com Galerkin, também chamado de método de Galerkin ou abordagem de Galerkin, é usado aqui.

Princípio do mínimo de energia potencial

Em sistemas conservadores , no caso de um problema estático, os deslocamentos nodais podem ser determinados a partir da condição de que a energia potencial tenha um mínimo no estado de equilíbrio desejado . Com o princípio do mínimo de energia potencial, as equações de rigidez dos elementos finitos podem ser determinadas diretamente. A energia potencial de uma estrutura é a soma da energia de deformação interna (a energia de deformação elástica) e o potencial das cargas aplicadas (o trabalho realizado por forças externas).

Método de comprimento de arco

O método do comprimento do arco é um método em que se pode calcular de forma controlada por força até a capacidade de carga máxima. A necessidade de métodos controlados por força é que, ao contrário dos métodos controlados por deslocamento, pode-se aumentar cargas múltiplas em proporção direta. Com o método do comprimento do arco, a carga é aumentada conforme especificado; Se esse aumento de carga levar a uma deformação muito grande, a carga é multiplicada por um fator menor que 1, e mesmo com valores negativos após o alcance da capacidade de carga.

Método estocástico de elementos finitos

Na variante do método dos elementos finitos estocásticos (SFEM), as variáveis ​​de entrada do modelo que estão sujeitas a uma incerteza, por exemplo, resistências ou cargas do material, são modeladas usando variáveis ​​estocásticas. Isso pode ser alcançado usando variáveis ​​aleatórias comuns . Os campos aleatórios também são freqüentemente usados, os quais são funções matemáticas contínuas e variáveis ​​aleatoriamente. Um método de cálculo comum é a simulação de Monte Carlo . O cálculo FE é repetido para muitas implementações aleatórias ( amostras ) das variáveis ​​de entrada até que uma caia abaixo de um certo erro estocástico definido antecipadamente. Os momentos, ou seja, valor médio e variância, são então calculados a partir de todos os resultados. Dependendo da distribuição das variáveis ​​de entrada, muitas repetições do cálculo FE são frequentemente necessárias, o que pode levar muito tempo de computação.

Solucionadores de FE implícitos e explícitos

Os sistemas FEM mecânicos estruturais são representados por sistemas lineares de equações de 2ª ordem:

${\ displaystyle M {\ ddot {u}} (t) + D {\ dot {u}} (t) + Ku (t) = P (t)}$

${\ displaystyle M, D}$e são a matriz de massa, amortecimento e rigidez do sistema; é o vetor das forças externas atuando no modelo. é o vetor dos graus de liberdade. ${\ displaystyle K}$${\ displaystyle P (t)}$${\ displaystyle u}$

Modelos de componentes complexos geralmente consistem em vários milhões de nós, e cada nó pode ter até 6 graus de liberdade. Solucionadores de FEM (solucionadores de sistema de equação) devem, portanto, atender a certos requisitos em relação ao gerenciamento de memória eficaz e, se necessário, ao uso de várias CPUs. Existem dois tipos fundamentalmente diferentes de solucionadores de FEM: implícitos e explícitos.

Os solucionadores de FEM implícitos fazem certas suposições sob as quais o vetor de solução calculado é válido. Atos z. B. uma carga temporalmente imutável em um sistema com amortecimento, então após um tempo suficientemente longo, um vetor de deslocamento constante será estabelecido. Pois é então , e o sistema de equações simplifica com a solução${\ displaystyle u}$${\ displaystyle P (t) = P = const.}$${\ displaystyle u (t) = u = const.}$${\ displaystyle t \ to \ infty}$${\ displaystyle {\ ddot {u}} (t) = {\ dot {u}} (t) = 0}$${\ displaystyle Ku = P}$${\ displaystyle u = K ^ {- 1} P}$

Para um determinado vetor de carga , o vetor de deslocamento pode ser calculado usando o algoritmo Gaussiano ou decomposição QR de . ${\ displaystyle P}$${\ displaystyle u}$${\ displaystyle K}$

Se um sistema mecânico for exposto à excitação harmônica , pode ser necessário determinar as frequências naturais do sistema para evitar ressonâncias durante a operação. ${\ displaystyle P (t) = {\ hat {P}} \ sin (\ Omega t)}$

Frequências naturais são todas as frequências para as quais um vetor de deslocamento representa uma solução do sistema de equações sem carga ( ) e sem amortecimento ( ). O seguinte então se aplica ao vetor de velocidade e aceleração ${\ displaystyle \ omega _ {i}}$${\ displaystyle u (t) = {\ hat {u}} _ {i} \ sin (\ omega _ {i} t)}$${\ displaystyle P (t) = 0}$${\ displaystyle D = 0}$

${\ displaystyle {\ dot {u}} _ {i} = {\ hat {u}} _ {i} \ \ omega _ {i} \ cos (\ omega _ {i} t), \ {\ ddot { u}} _ {i} = - {\ hat {u}} _ {i} \ omega _ {i} ^ {2} \ sin (\ omega _ {i} t)}$

e o sistema de equações é, portanto,

${\ displaystyle (-M \ omega _ {i} ^ {2} + K) {\ hat {u}} _ {i} \ sin (\ omega _ {i} t) = 0}$

Para calcular as frequências próprias e os modos próprios associados , o solucionador implícito deve resolver o problema dos valores próprios ${\ displaystyle \ omega _ {i}}$${\ displaystyle {\ hat {u}} _ {i}}$

${\ displaystyle -M \ omega _ {i} ^ {2} + K = 0}$

resolver.

Solucionadores explícitos do FEM

Os solucionadores explícitos calculam os vetores de deslocamento em certos pontos discretos no tempo dentro de um determinado intervalo de tempo. As velocidades e acelerações dos nós são aproximadas por quocientes de diferença dos deslocamentos em pontos sucessivos no tempo . Com um intervalo de tempo constante, o seguinte se aplica ${\ displaystyle u_ {i}}$${\ displaystyle t_ {i}}$${\ displaystyle u_ {i + 1}, u_ {i}, u_ {i-1}}$${\ displaystyle t_ {i + 1}, t_ {i}, t_ {i-1}}$${\ displaystyle t_ {i + 1} -t_ {i} = \ Delta \ t}$

${\ displaystyle {\ dot {u}} = {\ frac {u_ {i} -u_ {i-1}} {\ Delta \ t}}}$

${\ displaystyle {\ ddot {u}} = {\ frac {{\ frac {u_ {i + 1} -u_ {i}} {\ Delta \ t}} - {\ frac {u_ {i} -u_ { i-1}} {\ Delta \ t}}} {\ Delta \ t}} = {\ frac {u_ {i + 1} -2u_ {i} + u_ {i-1}} {(\ Delta t) ^ {2}}}}$

o sistema discretizado de equações tem a forma

${\ displaystyle M {\ frac {u_ {i + 1} -2u_ {i} + u_ {i-1}} {(\ Delta t) ^ {2}}} + D {\ frac {u_ {i} - u_ {i-1}} {\ Delta \ t}} + Ku_ {i} = P_ {i}}$

Ao resolver esta equação, é obtida uma relação com a qual o vetor de deslocamento pode ser determinado a partir dos vetores calculados anteriormente e : ${\ displaystyle u_ {i + 1}}$${\ displaystyle u_ {i}}$${\ displaystyle u_ {i-1}}$

${\ displaystyle u_ {i + 1} = M ^ {- 1} ((\ Delta t) ^ {2} (P_ {i} -Ku_ {i}) - D \ Delta \ t (u_ {i} -u_ {i-1})) + 2u_ {i} -u_ {i-1}}$

O cálculo do inverso não é realizado na prática, uma vez que os solucionadores explícitos geralmente assumem uma matriz diagonal e, portanto, cada linha do sistema de equações só precisa ser dividida pela entrada diagonal na linha correspondente de . ${\ displaystyle M ^ {- 1}}$${\ displaystyle M}$${\ displaystyle M}$

Solucionadores explícitos são usados, entre outras coisas, na construção de veículos para o cálculo de casos de carga de colisão.

A vantagem dos solucionadores diretos de equações de acordo com o método de Gauss está na aplicação prática na estabilidade numérica e no recebimento de um resultado exato. As desvantagens são o mau condicionamento das matrizes de rigidez geralmente pouco povoadas e os altos requisitos de armazenamento, conforme mencionado acima. Solucionadores iterativos são menos sensíveis ao condicionamento deficiente e requerem menos memória quando o armazenamento de elemento diferente de zero é usado. No entanto, solucionadores iterativos usam um critério de terminação para calcular os resultados. Se isso for alcançado antes de uma solução aproximadamente exata ter sido encontrada, o resultado, por exemplo, uma curva de tensão, pode ser facilmente mal interpretado.

Em algumas implementações, apenas as posições e valores das entradas que se desviam de zero são armazenados para as matrizes esparsas que ocorrem com frequência . Isso permite que você continue a resolver os sistemas de equações diretamente, mas economiza muito espaço na memória.

Análise isogeométrica

Alguns programas podem adaptar uma malha FE existente a uma geometria CAD (muito semelhante, nova), que geralmente é significativamente menor do que no caso de uma (pequena) alteração na geometria do componente (CAD). Tempo de computação necessário.

Programas

O software de elementos finitos e sua aplicação são agora uma indústria multibilionária.

• Na prática, muitos programas grandes independentes com uma gama semelhante de aplicativos estão em uso; a seleção de qual programa usar depende não só do uso, mas também de fatores como disponibilidade, padrão de certificação na empresa ou custos de licença.
• Com os pacotes de elementos finitos integrados em sistemas CAD comerciais , problemas mais simples (geralmente lineares) podem ser calculados e avaliados diretamente usando o sistema CAD. As etapas individuais, por exemplo B. o processo de rede ( malha ) é executado automaticamente em segundo plano.
• Como às vezes é necessário muito poder de computação para realizar o cálculo, as primeiras empresas estão disponibilizando poder de computação para seus usuários na forma de serviços em nuvem.
• Existem pré-processadores / pós-processadores com uma interface gráfica do usuário e solucionadores FE separados.
• Existem estruturas de programa sem uma interface gráfica de usuário, principalmente como um pré-processador com um solucionador de equações integrado, que são operados por linguagem de programação, por exemplo, para controlar o solucionador FE com rotinas adicionais feitas por ele mesmo.

Derivação matemática

A área de solução examinada é primeiro dividida em subáreas , os elementos finitos: ${\ displaystyle G}$${\ displaystyle G_ {1}, \ dotsc, G_ {m} \ subconjunto G}$

${\ displaystyle G = \ bigcup _ {e = 1} ^ {m} G_ {e}}$.

Dentro estão a função de solução desejada, funções de forma diferentes agora definidas, as quais são apenas alguns elementos iguais a zero, respectivamente. Esta propriedade é a verdadeira razão para o termo elementos "finitos". ${\ displaystyle G}$${\ displaystyle f \ colon G \ to \ mathbb {R} ^ {k}}$${\ displaystyle \ psi _ {1}, \ dotsc, \ psi _ {n} \ dois pontos G \ a \ mathbb {R} ^ {k}}$

As soluções possíveis da aproximação numérica são determinadas por uma combinação linear das funções de forma

${\ displaystyle f (x) = \ sum _ {i = 1} ^ {n} c_ {i} \ cdot \ psi _ {i} (x) \ quad, c_ {i} \ in \ mathbb {R}}$.

Uma vez que cada função de teste desaparece na maioria dos elementos, a função restrita ao elemento pode, inversamente , ser descrita pela combinação linear de menos funções de teste . ${\ displaystyle G_ {e}}$${\ displaystyle f | G_ {e}}$${\ displaystyle \ psi _ {i}}$

Se as equações diferenciais e as condições de contorno do problema podem ser representadas como operadores lineares em relação às funções , isso leva a um sistema linear de equações em relação às variáveis ​​livres da combinação linear : ${\ displaystyle f}$${\ displaystyle c_ {i}}$

${\ displaystyle D (c) = g}$

Com

${\ displaystyle D}$= Mapeamento linear de em um espaço funcional${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle c}$ = Vetor de fatores de combinação linear ${\ displaystyle c_ {i}}$

${\ displaystyle g}$ = Função que representa a equação diferencial e as condições de contorno

Para obter um sistema linear finito de equações, a faixa de valores também é modelada por meio de funções de abordagem . Então, o pode ser descrito usando combinações lineares : ${\ displaystyle D}$${\ displaystyle \ phi _ {1}, \ dotsc, \ phi _ {n}}$${\ displaystyle g}$${\ displaystyle \ phi _ {i}}$

${\ displaystyle g (x) = \ sum _ {i = 1} ^ {n} b_ {i} \ cdot \ phi _ {i} (x) \ quad, b_ {i} \ in \ mathbb {R}}$

e o sistema de equações é obtido globalmente

${\ displaystyle A \ cdot c = b}$

Com

${\ displaystyle A}$ = matriz quadrada com ${\ displaystyle A = \ phi ^ {- 1} \ cdot D}$

${\ displaystyle c}$ = Vetor de fatores de combinação linear ${\ displaystyle c_ {i}}$

${\ displaystyle b}$ = Vetor de fatores de combinação linear ${\ displaystyle b_ {i}}$

A dimensão da matriz resulta do número de funções de abordagem multiplicado pelos graus de liberdade em que o modelo físico é baseado . A dimensão da matriz é o número total de graus de liberdade, pelo que as especificações correspondentes ao modelo no que diz respeito à singularidade do problema (por exemplo, os deslocamentos do corpo rígido no caso de um corpo elástico) devem ser excluídas. ${\ displaystyle k}$

Como cada elemento está conectado apenas a alguns elementos vizinhos, a maioria dos valores da matriz geral é zero, de modo que ela é “esparsamente povoada”. Na maioria dos casos de uso, as mesmas funções são usadas como funções em lote e funções de teste . Nesse caso, a matriz também é simétrica em relação à sua diagonal principal . ${\ displaystyle \ psi _ {i}}$${\ displaystyle \ phi _ {i}}$

Se o número de graus de liberdade não for muito grande (até aproximadamente 500.000), este sistema de equações pode ser resolvido de forma mais eficiente usando um método direto , por exemplo, com o método de eliminação de Gauss . A estrutura esparsa do sistema de equações pode ser usada de forma eficaz aqui. Embora o esforço de cálculo para equações seja com o algoritmo de Gauss , o esforço pode ser significativamente reduzido por seleção inteligente de pivô (por exemplo, algoritmo de Markowitz ou abordagens teóricas de gráfico ). ${\ displaystyle N}$${\ displaystyle {\ mathcal {O}} (N ^ {3})}$

Para mais de 500.000 incógnitas, o mau estado do sistema de equações torna os solucionadores diretos cada vez mais difíceis, de modo que os solucionadores iterativos que melhoram uma solução passo a passo são geralmente usados ​​para problemas grandes . Exemplos simples disso são os métodos Jacobi e Gauss-Seidel , mas na prática métodos multigrid ou métodos de subespaço Krylow pré- condicionados , como o gradiente conjugado ou método GMRES , são usados. Devido ao tamanho dos sistemas de equação, às vezes é necessário usar computadores paralelos .

Se a equação diferencial parcial for não linear , o sistema de equações resultante também será não linear. Normalmente, isso só pode ser resolvido usando métodos de aproximação numérica. Um exemplo de tal método é o método de Newton , no qual um sistema linear é resolvido passo a passo.

Atualmente, há um grande número de programas de computador comerciais que usam o método dos elementos finitos.

Formulação fraca

Uma equação diferencial parcial elíptica pode ser formulada fracamente, i. H. o problema pode ser expresso de uma forma que requeira menos suavidade da solução . Ele faz isso da seguinte maneira.

Dado um espaço de Hilbert , um funcional (função de seu espaço dual) , bem como uma forma bilinear contínua e elíptica , então a solução do problema de variação é chamada se ${\ displaystyle H}$${\ displaystyle f \ in H ': = \ {g: \; H \ rightarrow \ mathbb {R} | \; g {\ text {é linear e contínuo}} \}}$${\ displaystyle H}$ ${\ displaystyle a (\ cdot, \ cdot)}$${\ displaystyle u \ in H}$

${\ displaystyle a (u, v) = f (v) \ \ forall v \ in H}$.

A existência e unicidade da solução fornece o teorema da representação Fréchet Riesz (para o caso em que a forma bilinear é simétrica) ou o lema Lax-Milgram (caso geral). ${\ displaystyle u}$${\ displaystyle a}$

Sabemos que o quarto é um quarto de Hilbert . Com base nisso, os espaços de Sobolew podem ser definidos usando a chamada derivada fraca . ${\ displaystyle L ^ {2} (\ Omega): = \ {f: \ Omega \ rightarrow \ mathbb {R} \ | \ \ | f \ | _ {L ^ {2}} <\ infty \}}$ ${\ displaystyle H ^ {s} (\ Omega)}$

O problema pode ser visto como uma variante de uma equação diferencial parcial em uma área . ${\ displaystyle a (u, v) = f (v)}$${\ displaystyle \ Omega}$

O problema de Poisson como exemplo:

${\ displaystyle - \ Delta u (x) = f (x) \ \ forall x \ in \ Omega}$

${\ displaystyle u (x) = 0 \ \ forall x \ in \ partial \ Omega}$

onde aqui denota o operador Laplace . Uma multiplicação com funções continuamente diferenciáveis ​​infinitamente frequentemente resulta após uma integração ${\ displaystyle \ Delta}$${\ displaystyle \ psi \ in C_ {0} ^ {\ infty} (\ Omega)}$

${\ displaystyle \ Leftrightarrow - \ int _ {\ Omega} \ Delta u \, \ psi \, dx = \ int _ {\ Omega} f \, \ psi \, dx \ \ forall \ psi \ in C_ {0} ^ {\ infty} (\ Omega).}$

Uma integração parcial ( fórmula do Primeiro Green ) e as condições de limite zero para então entregar ${\ displaystyle \ psi}$

${\ displaystyle \ Leftrightarrow \ int _ {\ Omega} \ nabla u \, \ nabla \ psi \, dx = \ int _ {\ Omega} f \, \ psi \, dx \ \ forall \ psi \ in C_ {0 } ^ {\ infty} (\ Omega)}$

Agora, uma forma bilinear elíptica e contínua está ativada , e o lado direito é uma forma linear contínua${\ displaystyle a (u, \ psi): = \ int _ {\ Omega} \ nabla u \, \ nabla \ psi \, dx}$${\ displaystyle H_ {0} ^ {1} (\ Omega): = {\ overline {C_ {0} ^ {\ infty} (\ Omega)}} ^ {\ | \ cdot \ | _ {H ^ {1 }}}}$${\ displaystyle (f, \ psi) _ {L ^ {2}} = f (\ psi)}$${\ displaystyle H_ {0} ^ {1} (\ Omega)}$

Se o espaço de funções / espaço de Hilbert em consideração tem uma base finita, um sistema linear de equações pode ser obtido a partir da formulação da variação.

Para salas funcionais, a escolha da base determina a eficiência do processo. O uso de splines com triangulações e, em certos casos, a transformação discreta de Fourier (divisão em seno e cosseno) são comuns aqui.

Devido a considerações de flexibilidade em relação à geometria da área , geralmente é escolhida a seguinte abordagem. ${\ displaystyle \ Omega}$

A área é discretizada dividindo-a em triângulos e usando splines associadas aos vértices p para abranger o espaço de função de dimensão finita . As splines se encontram em pontos especificados nos triângulos (onde δ é o delta de Kronecker ). Então você pode representar uma função discreta por meio de ${\ displaystyle \ Omega}$${\ displaystyle \ lambda _ {p} (x)}$${\ displaystyle \ Omega}$${\ displaystyle \ lambda _ {p} (q) = \ delta _ {pq}}$${\ displaystyle u_ {h} (x)}$

${\ displaystyle u_ {h} (x) = \ sum _ {p} u_ {p} \, \ lambda _ {p} (x)}$

com os coeficientes relacionados à representação básica. Devido à base finita, você não precisa mais testar contra todas , mas apenas contra todas as funções de base; a formulação das variações é reduzida devido à linearidade ${\ displaystyle u_ {p}}$${\ displaystyle \ psi \ in H_ {0} ^ {1}}$

${\ displaystyle a (u_ {h}, \ lambda _ {q}) = \ sum _ {p} u_ {p} \, a (\ lambda _ {p}, \ lambda _ {q}) = (f, \ lambda _ {q}) \ \ forall q}$

Então, temos um sistema de equações lineares para resolver

${\ displaystyle A \ cdot u = f}$,

Com

${\ displaystyle A_ {pq} = a (\ lambda _ {p}, \ lambda _ {q})}$

e

${\ displaystyle f_ {q} = (f, \ lambda _ {q})}$

Este resultado é obtido com todas as bases finitas do espaço de Hilbert.

exemplo

Definição formal do elemento finito (de acordo com Ciarlet )

Um elemento finito é um triplo , onde: ${\ displaystyle E = (T, \ Pi, \ Sigma)}$

• ${\ displaystyle T}$ é uma área não vazia (por exemplo, triângulos, quadrados, tetraedros, etc.)
• ${\ displaystyle \ Pi}$é um espaço de dimensão finita de funções de forma (funções de forma linear, quadrática ou cúbica, ou seja, ranhuras; senos, etc.) funções de forma${\ displaystyle \ rightarrow}$
• ${\ displaystyle \ Sigma}$é um conjunto de funcionais linearmente independentes em variáveis ​​de nó${\ displaystyle \ Pi}$ ${\ displaystyle \ rightarrow}$

Aplica-se aos funcionais que estão associados às funções da base:

${\ displaystyle \ sigma _ {i} \ in \ Sigma: \ sigma _ {i} (\ pi _ {j}) = \ delta _ {ij} \ \ j \ in \ {1, \ ldots, \ dim ( \ Pi) \}}$

Então se aplica a todas as funções

${\ displaystyle v \ in \ Pi: v (x) = \ sum _ {i} \ sigma _ {i} (x) \, \ pi _ {j}}$.

Para seno como a função de base, im é então ${\ displaystyle \ mathbb {(} R) ^ {1}}$

${\ displaystyle \ operatorname {span} \, \ left \ {\ sin (x), \ sin (2x), \ ldots, \ sin (nx) \ right \} = \ Pi}$

e o funcional

${\ displaystyle \ sigma _ {i} (\ psi): = (\ sin (ix), \ psi) _ {L ^ {2}}}$.

Para estrias, no entanto, a avaliação ponto sobre os pontos dos triângulos especificados é suficiente: . ${\ displaystyle \ sigma _ {p} (\ psi): = \ psi (p)}$

S1: Elementos lineares em triângulos

O espaço FEM de funções lineares contínuas por partes é definido como:

${\ displaystyle S ^ {1} (\ Omega, T): = \ left \ lbrace u \ in C ^ {0} (\ Omega) \; | \; {u |} _ {\ Delta} (x, y ) = a _ {\ Delta} + b _ {\ Delta} x + c _ {\ Delta} y \ quad \ forall \ Delta \ in T \ right \ rbrace}$,

onde é uma região e a triangulação da região com triângulos e denota a restrição da função contínua ao triângulo . ${\ displaystyle \ Omega \ subset \ mathbb {R} ^ {2}}$${\ displaystyle T \ subset \ Omega}$${\ displaystyle \ Delta}$${\ displaystyle {u |} _ {\ Delta}}$${\ displaystyle u}$${\ displaystyle \ Delta \ in T}$

P1: Elemento de referência linear em um triângulo

O elemento de referência é definido como: ${\ displaystyle {\ hat {T}}}$

${\ displaystyle {\ hat {T}} = \ left \ lbrace (x, y) \ in \ mathbb {R} ^ {2} | 0 <x <1 \; {\ text {and}} \; 0 < y <1-x \ right \ rbrace.}$

Os elementos lineares são funções do tipo: ${\ displaystyle P1}$

${\ displaystyle p \ colon {\ hat {T}} \ to \ mathbb {R}, (x, y) \ mapsto a + bx + cy \ quad {\ text {with}} \; a, b, c \ em \ mathbb {R}.}$

Para definir a função, é suficiente especificar os valores nos pontos dos cantos . Portanto, todas as funções podem ser representadas usando funções básicas : ${\ displaystyle p}$${\ displaystyle {\ has {E_ {1}}}: = (0,0), {\ has {E_ {2}}}: = (1,0), {\ has {E_ {3}}}: = (0,1)}$${\ displaystyle p}$${\ displaystyle {\ hat {\ phi}} _ {i}}$

${\ displaystyle p (x, y) = \ sum _ {i = 1} ^ {3} \ alpha _ {i} {\ hat {\ phi}} _ {i} (x, y) \ quad {\ text {com}} \; \ alpha _ {i} \ in \ mathbb {R}.}$

As funções básicas são fornecidas como funções lineares que só são diferentes de zero em um ponto de canto:

${\ displaystyle {\ hat {\ phi}} _ {i} ({\ hat {E_ {j}}}) = \ delta _ {i, j} \ quad \ forall i, j = 1,2,3}$

onde está a função delta de Kronecker . ${\ displaystyle \ delta}$

Transformação do elemento de referência

Para vincular o elemento de referência com um triângulo arbitrário (vértices :), usa-se uma transformação linear : ${\ displaystyle T}$${\ displaystyle E_ {1}, E_ {2}, E_ {3}}$ ${\ displaystyle F_ {T}}$

${\ displaystyle {\ begin {alinhado} F_ {T} & \ colon {\ hat {T}} \ to T, \ quad F (v) = B_ {T} v + b_ {T} \\ B_ {T} &: = \ left (E_ {2} -E_ {1}, E_ {3} -E_ {1} \ right), \ quad b_ {T}: = E_ {1}. \ end {alinhados}}}$

Em muitos problemas relacionados a equações diferenciais parciais , o produto escalar das funções de base (definidas em qualquer triângulo ) deve ser calculado: ${\ displaystyle L ^ {2}}$${\ displaystyle \ phi _ {i}}$${\ displaystyle T}$

${\ displaystyle (\ nabla \ phi _ {i}, \ nabla \ phi _ {j}) _ {L ^ {2} (T)} = \ int _ {T} \ nabla \ phi _ {i} (x ) \ cdot \ nabla \ phi _ {j} (x) dx.}$

Com a ajuda do conjunto de transformação , a integração pode ser deslocada para o elemento de referência:

${\ displaystyle \ int _ {T} \ nabla \ phi _ {i} (x) \ cdot \ nabla \ phi _ {j} (x) dx = \ int _ {\ hat {T}} \ left (\ left (DF_ {T} (z) \ right) ^ {- T} \ nabla {\ hat {\ phi}} _ {i} (z), \ left (DF_ {T} (z) \ right) ^ {- T} \ nabla {\ hat {\ phi}} _ {j} (z) \ direita) _ {\ mathbb {R} ^ {2}} | \ det DF_ {T} (z) | dz.}$

literatura

• Martin Mayr / Ulrich Thalhofer: Métodos de solução numérica na prática: FEM-BEM-FDM . Hanser, 1993, ISBN 3-446-17061-8 , pp. 312 . 
• JN Reddy: Princípios de energia e métodos variacionais em mecânica aplicada . 2ª Edição. John Wiley & Sons, 2002, ISBN 0-471-17985-X . 
• D. Braess: Teoria dos Elementos Finitos, Soluções Rápidas e Aplicações na Teoria da Elasticidade . 4ª edição. Springer, 2007, ISBN 978-3-540-72449-0 . 
• Günter Müller (Ed.): FEM para praticantes . 4 volumes. Expert Verlag, Renningen. 
  • Volume 1: Fundamentos: Conhecimento básico e exemplos de trabalho para aplicações FEM. 2007, ISBN 978-3-8169-2685-6 .
  • Volume 2: Dinâmica Estrutural. 2008, ISBN 978-3-8169-2842-3 .
  • Volume 3: Campos de temperatura. 2007, ISBN 978-3-8169-2714-3 .
  • Volume 4: Engenharia Elétrica. 2009, ISBN 978-3-8169-2841-6 .
• Klaus-Jürgen Bathe: Métodos de Elementos Finitos . 2ª Edição. Springer-Verlag, 2002, ISBN 3-540-66806-3 . 
• WE Gawehn: Método dos Elementos Finitos . BOD Book on Demand, 2009, ISBN 978-3-8370-2497-5 (conceitos básicos do FEM para estática e dinâmica). 
• Frank Rieg, Reinhard Hackenschmidt, Bettina Alber-Laukant: Análise de Elementos Finitos para Engenheiros: Uma introdução fácil de entender . Hanser Fachbuchverlag, 2012, ISBN 978-3-446-42776-1 (aplicação de FEM em engenharia). 
• René de Borst , Mike Crisfield , Joris Remmers, Clemens Verhoosel: Nonlinear finite element analysis of solid and structure , Wiley-VCH 2014
• Karl-Eugen Kurrer : A História da Teoria das Estruturas. Searching for Equilibrium , Ernst and Son 2018, pp. 881-914, ISBN 978-3-433-03229-9

Links da web

• O método dos elementos finitos em biomedicina, biomecânica e áreas afins.
• Métodos numéricos (palestra e estágio, roteiro) ( Memento de 20 de outubro de 2018 no Internet Archive )
• FU Mathiak: O método dos elementos finitos (FEM). ( Memento de 26 de novembro de 2019 no Internet Archive ) [PDF; 3,86 MB].

Evidência individual

1. ^ Karl Schellbach: Problemas do cálculo das variações . In: Jornal de matemática pura e aplicada . fita 41 , no. 4 , 1852, pp. 293-363 . 
2. ↑ Ernst Gustav Kirsch: As equações fundamentais da teoria da elasticidade dos corpos sólidos, derivadas da consideração de um sistema de pontos que são conectados por escoras elásticas. In: Journal of the German Engineers , Volume 7 (1868), Issue 8.
3. ^ John William Strutt: Na teoria da ressonância . In: Philosophical Transactions of the Royal Society of London . fita 161 , 1871, pp. 77-118 . 
4. ↑ Walter Ritz: Sobre um novo método para resolver certos problemas de variação em física matemática . In: Jornal de matemática pura e aplicada . fita 135 , 1909, pp. 1-61 . 
5. ↑ Christoph Haderer: Estudos de extensão e parâmetros de um código de elemento finito estocástico 1-D com campos aleatórios. Grupo de Análise de Risco de Engenharia. Universidade Técnica de Munique, 2017.
6. ^ David Roylance: Análise de elementos finitos. (PDF; 348 kB), acessado em 10 de maio de 2017.