Projeção (álgebra linear)

O mapeamento linear T é a projeção ao longo de k em m. Todos os pontos na imagem m (por exemplo, w ) são mapeados por T em si mesmo (por exemplo, Tw ).

Em matemática , uma projeção ou projetor é um mapeamento linear especial ( endomorfismo ) sobre um espaço vetorial que deixa todos os vetores em sua imagem (um subespaço de ) inalterados. ${\ displaystyle V}$${\ displaystyle V}$

Se uma base de for escolhida apropriadamente , a projeção define alguns componentes de um vetor para zero e mantém os outros. Isso justifica claramente o termo projeção, como a ilustração de uma casa em uma planta bidimensional. ${\ displaystyle V}$

definição

Deixe ser um espaço vetorial . Um endomorfismo de espaço vetorial é chamado de projeção se for idempotente , ou seja, se for válido. ${\ displaystyle V}$ ${\ displaystyle P \ dois pontos V \ a V}$${\ displaystyle P \ circ P = P}$

características

Uma projeção só pode ter os números 0 e 1 como autovalores . Os eigenspaces são

• ${\ displaystyle \ ker P}$( Núcleo de ) para o autovalor 0 e${\ displaystyle P}$
• ${\ displaystyle \ operatorname {im} P}$( Imagem de ) para o autovalor 1.${\ displaystyle P}$

O espaço total é a soma direta desses dois subespaços :

${\ displaystyle V = \ ker P \ oplus \ operatorname {im} P}$

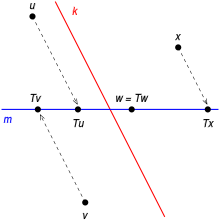
A ilustração fala claramente uma projeco paralela ao longo . ${\ displaystyle P}$${\ displaystyle \ operatorname {im} P}$${\ displaystyle \ ker P}$

Se houver uma projeção, então também haverá uma projeção, e o seguinte se aplica: ${\ displaystyle P}$${\ displaystyle \ operatorname {id} -P}$

${\ displaystyle \ ker P = \ operatorname {im} (\ operatorname {id} -P)}$

${\ displaystyle \ operatorname {im} P = \ ker (\ operatorname {id} -P)}$

Projeções e complementos

Se existe um espaço vetorial e um subespaço, então, em geral, existem muitas projeções sobre , isto é, projeções cuja imagem é. Se houver uma projeção com uma imagem , há um complemento para in . ${\ displaystyle V}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle P}$${\ displaystyle U}$${\ displaystyle \ ker P}$${\ displaystyle U}$${\ displaystyle V}$

Por outro lado, se um complemento de em , então , cada um pode ser uma soma com claramente especificado e representar. O endomorfismo de , que atribui o que pertence a cada um , é uma projeção com uma imagem e um núcleo . As projeções e decomposições em subespaços complementares correspondem umas às outras. ${\ displaystyle W}$${\ displaystyle U}$${\ displaystyle V}$${\ displaystyle V = U \ oplus W}$${\ displaystyle v \ in V}$${\ displaystyle v = u + w}$${\ displaystyle u \ in U}$${\ displaystyle w \ in W}$${\ displaystyle V}$${\ displaystyle v}$${\ displaystyle u}$${\ displaystyle U}$${\ displaystyle W}$

Projeção ortogonal

Decomposição ortogonal de um vetor em uma parte em um plano e uma parte no complemento ortogonal do plano${\ displaystyle v}$${\ displaystyle P (v) = u}$${\ displaystyle U}$${\ displaystyle vP (v) = u ^ {\ perp}}$${\ displaystyle U ^ {\ perp}}$

Se for um espaço vetorial de dimensão finita real ou complexo com um produto escalar , há uma projeção ao longo do complemento ortogonal de para cada espaço sub-vetorial , que é chamada de "projeção ortogonal em ". É o mapeamento linear determinado exclusivamente com a propriedade que para todos${\ displaystyle V}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle P \ dois pontos V \ a V}$${\ displaystyle v \ in V}$

• ${\ displaystyle P (v) \ in U}$ e
• ${\ displaystyle vP (v) \ perp U}$

se aplica.

Se for um espaço de Hilbert de dimensão infinita , então esta afirmação com o teorema da projeção se aplica de acordo com espaços subvetoriais fechados . Nesse caso, contínuo pode ser escolhido. ${\ displaystyle V}$${\ displaystyle U}$${\ displaystyle P}$

Exemplos

Como exemplos simples podem ser para cada espaço vetorial a identidade e a figura para o estado como projeções triviais (que podem ser representadas pela unidade ou matriz zero). ${\ displaystyle V}$${\ displaystyle Id: v \ mapsto v}$${\ displaystyle N \ dois pontos v \ mapsto 0}$${\ displaystyle v \ in V}$

Que seja o mapeamento do plano em si que é passado pela matriz ${\ displaystyle P}$${\ displaystyle \ mathbb {R} ^ {2}}$

${\ displaystyle P = {\ begin {pmatrix} 1 e 0 \\ 0 & 0 \ end {pmatrix}}}$

é descrito. Ele projecta um vector sobre , isto é, ortogonalmente sobre o eixo x. O espaço próprio para o valor próprio , isto é, o núcleo, é medido por , o espaço próprio para o valor próprio , ou seja, a imagem é expandida por. O projetor é a projeção ortogonal no eixo y. ${\ displaystyle {\ tbinom {x} {y}}}$${\ displaystyle {\ tbinom {x} {0}}}$${\ displaystyle 0}$${\ displaystyle {\ tbinom {0} {1}}}$${\ displaystyle 1}$${\ displaystyle {\ tbinom {1} {0}}}$${\ displaystyle \ operatorname {id} -P}$

Em contraste, por exemplo, é através da matriz

${\ displaystyle P = {\ begin {pmatrix} 1 e -1 \\ 0 & 0 \ end {pmatrix}}}$

A imagem descrita do plano também se deve a uma projeção, mas não a uma projeção ortogonal. Sua imagem é novamente o eixo x, mas seu núcleo é a linha reta com a equação . ${\ displaystyle P ^ {2} = P}$${\ displaystyle y = x}$

inscrição

Em mecânica quântica , em conexão com o processo de medição , fala-se de uma projeção do vetor de estado ψ, a interpretação precisa sendo descrita a seguir:

• Como resultado da medição , apenas um de i vem. A. questão um número infinito de assim chamados valores próprios dos observados observáveis (isto é, da atribuído autoadjunto operador no espaço de estado do sistema, o chamado espaço de Hilbert ). A seleção é feita aleatoriamente ( interpretação de Copenhagen ) com uma certa probabilidade, que não é exigida aqui.
• O cálculo da probabilidade de um autovalor (resultado da medição) ocorre, entre outras coisas, com o auxílio da projeção em seu autovalor .

A totalidade dos operadores de projeção obtidos desta forma é “completa” para um determinado mensurando e resulta na chamada representação espectral dos observáveis.

inchar

• Gerd Fischer : Linear Algebra. Vieweg-Verlag, ISBN 3-528-03217-0 .
• Dirk Werner : Análise Funcional. 6ª edição corrigida, Springer-Verlag, Berlin 2007, ISBN 978-3-540-72533-6 , página 161.