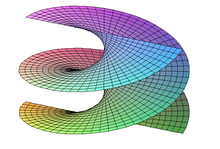
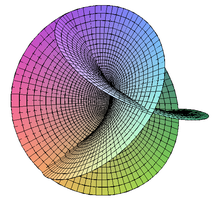
Área mínima

Uma área mínima é uma área no espaço que possui uma área mínima localmente . Essas formas assumem, por exemplo, películas de sabão quando são esticadas sobre uma moldura correspondente (como um anel de sopro).

Em termos matemáticos, as áreas mínimas são os pontos críticos da área funcional

${\ displaystyle A (\ mathbf {x}) = \ int {\ sqrt {g (u)}} \, \ mathrm {d} ^ {n} u}$.

Aqui estão os tamanhos e para declarados (ver. Matriz de Hessian ). Observe que uma área mínima não necessariamente tem uma área mínima, mas é apenas um ponto estacionário da área funcional. Pode-se mostrar que o desaparecimento da primeira variação da área funcional em duas dimensões espaciais é equivalente ao desaparecimento da curvatura média H se a variedade em consideração for suficientemente regular. ${\ displaystyle g (u): = \ operatorname {det} (g_ {ij} (u)) _ {i, j = 1, \ dotsc, n}}$${\ displaystyle g_ {ij} (u) = \ left ({\ tfrac {\ partial \ mathbf {x}} {\ partial u_ {i}}} \ right) ^ {T} {\ tfrac {\ partial \ mathbf {x}} {\ u_ parcial {j}}}}$${\ displaystyle i, j = 1, \ dotsc, n}$

A pesquisa matemática tem se concentrado em áreas mínimas desde o século XIX. Os experimentos do físico belga Joseph Plateau deram uma contribuição significativa para isso .

Explicações sobre a teoria existencial em duas variáveis

Uma área bidimensional de parâmetros sempre representa uma especialidade, porque com as ferramentas da teoria das funções pode-se obter enunciados muito mais extensos do que em dimensões espaciais superiores. Isso significa, por exemplo, que você sempre pode usar o disco circular como uma área de parâmetro com o teorema de mapeamento de Riemann . O teorema da uniformidade também se aplica apenas a duas dimensões espaciais. Permite introduzir parâmetros isotérmicos que são requeridos para a solução no caso paramétrico. É por isso que a teoria é particularmente bem desenvolvida em duas variáveis.

Formulação como um problema de variação

Uma superfície é uma superfície mínima se e somente se tiver curvatura média zero em todos os pontos . Assim, uma superfície mínima se apresenta como um caso especial de superfície com curvatura média prescrita, que também não escapam ao cálculo das variações , são mínimos do funcional de Hildebrandt.

${\ displaystyle A (\ mathbf {x}) = \ iint {\ big (} | \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v} | +2 (Q (\ mathbf {x }), \ mathbf {x} _ {u}, \ mathbf {x} _ {v}) {\ big)} \, \ mathrm {d} u \, \ mathrm {d} v}$.

As equações de Euler como as condições mínimas necessárias deste funcional são o sistema de superfície H em homenagem a Franz Rellich

${\ displaystyle \ Delta \ mathbf {x} = 2H \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v}, \ qquad \ mathbf {x} _ {u} ^ {2} - \ mathbf {x} _ {v} ^ {2} = 0 = \ mathbf {x} _ {u} \ mathbf {x} _ {v}}$.

Aqui está a curvatura média. ${\ displaystyle H = \ operatorname {div} \, Q}$

Caso paramétrico

Para este funcional, surge a questão da existência de mínimos locais com uma dada curva de contorno contínua de comprimento finito. Essa tarefa também é referida na literatura como o problema de Plateau. Assumindo uma condição de pequenez para a curvatura média, que é sempre cumprida no caso da área mínima, esta questão pode ser respondida positivamente. Para se convencer disso, minimiza-se e a energia funcional ao mesmo tempo${\ displaystyle A}$

${\ displaystyle E (\ mathbf {x}) = \ iint {\ Big (} {\ frac {1} {2}} | \ nabla \ mathbf {x} | ^ {2} +2 (Q (\ mathbf { x}), \ mathbf {x} _ {u}, \ mathbf {x} _ {v}) {\ Big)} \, \ mathrm {d} u \, \ mathrm {d} v}$

com a introdução dos chamados parâmetros quase isotérmicos.

Em 1884, Hermann Amandus Schwarz provou a sentença

No conjunto de superfícies orientáveis continuamente diferenciáveis , simplesmente fechadas, de gênero zero (ou seja, sem orifícios), a esfera é a superfície que delimita o maior volume para uma determinada superfície.

Pontos de ramificação

Os pontos em que a solução é satisfeita são chamados de pontos de ramificação. Os pontos de ramificação são interessantes porque a parametrização pode se tornar singular nesses pontos . Pior ainda é a possibilidade de que a solução local não seja mais uma superfície, mas apenas uma curva. ${\ displaystyle | \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v} | = 0}$

Considerações teóricas da função, que são essencialmente inspiradas no trabalho de Carleman e Vekua , mostram que a solução pode ter no máximo um número finito de tais pontos de ramificação. Infelizmente, o método acima não exclui esses pontos de ramificação a priori. Somente com o elaborado teorema de Gulliver-Alt- Osserman isso sucede a posteriori. Portanto, há um desejo de resolver o problema do platô na classe das superfícies H sem pontos de ramificação. Esta ainda é uma questão em aberto até hoje.

Caso não paramétrico, equação de área mínima

O método acima só leva ao sucesso para os constantes . Se a curvatura média também depende da solução, algo ainda pode ser feito no caso de um gráfico : Se um gráfico for, ele é escrito como e a função cumpre a equação não paramétrica da curvatura média prescrita${\ displaystyle H}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {x} (u, v) = (u, v, \ zeta (u, v)) ^ {T}}$${\ displaystyle \ zeta}$

${\ displaystyle (1+ \ zeta _ {v} ^ {2}) \ zeta _ {uu} -2 \ zeta _ {u} \ zeta _ {v} \ zeta _ {uv} + (1+ \ zeta _ {u} ^ {2}) \ zeta _ {vv} = H (u, v, \ zeta (u, v))}$.

No caso de áreas mínimas, H = 0 e a equação é chamada de equação de área mínima.

Um resultado de existência profunda fornece a solubilidade do problema de Dirichlet desta equação diferencial parcial, também sob a suposição de uma condição de pequenez e outros pré-requisitos técnicos. A singularidade também é esclarecida por um princípio máximo para a diferença entre duas soluções. Além disso, os gráficos são devidos a

${\ displaystyle | \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v} | = {\ sqrt {1+ \ nabla \ zeta (u, v) ^ {2}}} \ geq 1 }$

sempre livre de pontos de ramificação.

Exemplos de áreas mínimas

Vários exemplos de várias superfícies mínimas no espaço euclidiano tridimensional são dados aqui. Alguns deles não podem ser inseridos em um espaço tridimensional sem autocortes. Outros não podem continuar continuamente até o limite de seu domínio, como mostra o primeiro exemplo.

A área mínima de HF Scherk

A área mínima de Heinrich Ferdinand Scherk (1835): Estamos procurando todas as soluções para a equação da área mínima não paramétrica que podem ser escritas na forma e que satisfaçam as condições . Primeiro, inserimos esta estrutura na equação da área mínima e obtemos: ${\ displaystyle z = \ zeta {\ big (} u, v {\ big)} = f (u) + g (v)}$${\ displaystyle \ zeta {\ big (} 0,0 {\ big)} = 0}$${\ displaystyle \ nabla \ zeta (0,0) = 0}$

${\ displaystyle 0 \, \, = (1+ \ zeta _ {v} ^ {2}) \ zeta _ {uu} -2 \ zeta _ {u} \ zeta _ {v} \ zeta _ {uv} + (1+ \ zeta _ {u} ^ {2}) \ zeta _ {vv}}$

${\ displaystyle = {\ big (} 1+ (g '(v)) ^ {2} {\ big)} f' '(u) + (1+ (f' (u)) ^ {2}) g '' (v)}$

A conversão equivalente fornece

${\ displaystyle - {\ frac {f '' (u)} {1+ (f '(u)) ^ {2}}} = c = {\ frac {g' '(v)} {1+ (g '(v)) ^ {2}}}}$

com um . De acordo com a teoria das equações diferenciais ordinárias, há exatamente uma solução para cada um dos problemas de valor inicial ${\ displaystyle c \ in \ mathbb {R}}$

${\ displaystyle f '' {\ big (} u {\ big)} + c (1+ (f '(u)) ^ {2}) = 0}$ para os dados ${\ displaystyle f (0) = 0, \, \, f '(0) = 0}$

e

${\ displaystyle g '' {\ big (} v {\ big)} - c (1+ (g '(v)) ^ {2}) = 0}$ para os dados ${\ displaystyle g (0) = 0, \, \, g '(0) = 0}$

Essas soluções são

${\ displaystyle f (u) = {\ frac {1} {c}} \ log \ cos (cu)}$

e

${\ displaystyle g (v) = - {\ frac {1} {c}} \ log \ cos (cv).}$

Deve-se notar aqui que ainda podemos variar os valores iniciais e com um . No entanto, oBdA pode ser exigido devido à condição estrutural e ao fato de que as próprias funções não aparecem nas equações diferenciais ordinárias . Então temos: ${\ displaystyle f {\ big (} 0) = d}$${\ displaystyle g {\ big (} 0) = - d}$${\ displaystyle d \ in \ mathbb {R}}$${\ displaystyle d = 0}$

${\ displaystyle z = \ zeta {\ big (} u, v {\ big)} = f (u) + g (v) = {\ frac {1} {c}} \ log {\ frac {\ cos ( cu)} {\ cos (cv)}}}$

Notamos que esta área mínima está nos quadrados

${\ displaystyle \ Omega: = {\ big \ {} (u, v) \ in \ mathbb {R} ^ {2}: \, {\ big |} u + k {\ frac {\ pi} {c} } {\ big |} <{\ frac {\ pi} {2c}}, {\ big |} v + l {\ frac {\ pi} {c}} {\ big |} <{\ frac {\ pi } {2c}} \ quad {\ text {para}} \ quad k, l \ in \ mathbb {Z} \ quad {\ text {com}} \ quad k \ equiv l {\ pmod {2}} {\ grande \}}}$

explicado e não pode ser continuado além disso. Esta área pode ser incorporada como um gráfico no espaço tridimensional.

O catenóide

Se você deixar a linha da cadeia girar em torno do eixo x, também obterá uma área mínima embutida no espaço tridimensional - um catenóide. Catenóides são as únicas superfícies mínimas que também são superfícies de revolução ao mesmo tempo. Eles são suficientes para um parâmetro positivo c> 0 da equação

${\ displaystyle {\ sqrt {x ^ {2} + y ^ {2}}} = c \, \ operatorname {cosh} {\ frac {z} {c}}.}$

Foi uma das primeiras soluções experimentais de Plateau para o problema de Plateau. Aqui, os dados da borda eram dois anéis circulares, que formam a curva das bordas superior e inferior de um cone ou cilindro truncado.

O catenóide como superfície mínima vem de Leonhard Euler por volta de 1740.

A superfície helicoidal

A superfície helicoidal ou helicoidal está intimamente relacionada ao catenóide. Essa superfície emerge de um catenóide por meio de uma deformação descontínua, mas isométrica . Para um parâmetro c> 0, ele satisfaz as seguintes equações:

${\ displaystyle x {\ big (} u, v) = u \ cos v}$

${\ displaystyle y {\ big (} u, v) = u \ sin v}$

${\ displaystyle z {\ big (} u, v) = cv}$

Essa área mínima também está inserida no espaço tridimensional.

A superfície espiral como uma superfície mínima vem de Jean-Baptiste Meusnier de la Place (1776). As helicoides têm o gênero topológico 0. Na década de 1990, David Allen Hoffman e colegas construíram superfícies mínimas completas com gênero topológico finito infinito e arbitrário que poderiam ser embutidas no espaço euclidiano tridimensional com o auxílio de computadores , sendo a prova estrita apenas gênero infinito e para gênero 1 ( Michael Wolf , Hoffman, Matthias Weber 2009). Para o gênero 0, os helicoides (que também incluem os catenóides como um caso especial) e o plano são as únicas superfícies mínimas completamente incorporáveis ​​( William Meeks , Harold William Rosenberg 2005).

A área de Henneberg

A superfície de Henneberg é um exemplo de superfície mínima que é a imagem de uma imersão no espaço euclidiano tridimensional, mas não pode ser embutida no espaço euclidiano tridimensional. Suas equações determinantes são:

${\ displaystyle x (u, v) = 2 \ sinh u \ cos v - {\ frac {2} {3}} \ sinh (3u) \ cos (3v)}$

${\ displaystyle y (u, v) = 2 \ sinh u \ sin v + {\ frac {2} {3}} \ sinh (3u) \ sin (3v)}$

${\ displaystyle z (u, v) = 2 \ cosh (2u) \ cos (2v)}$

Além disso, essa superfície não pode ser orientada: em termos claros, não se pode decidir qual lado dessa superfície está para cima e qual é para baixo .

Tem o nome de Lebrecht Henneberg , que o apresentou em sua dissertação em 1875.

Dimensões superiores da sala

Em salas grandes, o acesso ao problema do planalto é difícil de imaginar. Aqui você só tem a opção de interpretar a solução como um gráfico. A equação da área mínima para o gráfico está escrita

${\ displaystyle \ operatorname {div} {\ frac {\ nabla \ zeta} {\ sqrt {1+ \ nabla \ zeta ^ {2}}}} = 0}$.

Com a teoria da fraca solubilidade de problemas de valor de contorno elíptico pode-se garantir a existência de soluções também nesta situação. As seguintes considerações de regularidade fornecem uma solução clássica. Como em duas dimensões espaciais, a unicidade também é obtida aqui por meio de um princípio de máximo para a diferença entre duas soluções.

Algumas declarações interessantes sobre áreas mínimas

Devido à estrutura relativamente simples das equações, que são satisfeitas por áreas mínimas, pode-se transferir algumas declarações conhecidas, que são conhecidas especialmente para funções holomórficas ou harmônicas, para áreas mínimas em duas variáveis.

Princípio máximo

A desigualdade vale para uma área mínima${\ displaystyle \ mathbf {x}}$

${\ displaystyle \ sup _ {w \ in B} | \ mathbf {x} (w) | \ leq \ sup _ {w \ in \ partial B} | \ mathbf {x} (w) |}$.

A área mínima, portanto, assume seu máximo na borda da área em que é declarada.

Uniformização de imagens

Os chamados parâmetros isotérmicos podem ser introduzidos na geodésia. O mapeamento que realiza isso é chamado de mapeamento de uniformização. Uniformizar imagens de áreas mínimas são funções harmoniosas .

Caráter analítico real

Enquanto estiverem presentes em parâmetros isotérmicos, as áreas mínimas são funções analíticas reais no interior da área em que são explicadas. Isso significa que a representação paramétrica pode ser expandida em uma série de potências convergentes em qualquer ponto na área nas proximidades desse ponto . Portanto, ele pode ser diferenciado várias vezes . Se, além disso, a curva limite for analítica real em um ponto, então a área mínima na vizinhança desse ponto pode ser continuada além da aresta usando análise real.

Os teoremas de Bernstein e Liouville

O teorema de Sergei Bernstein para superfícies mínimas é:

Uma solução totalmente explicada da equação de área mínima não paramétrica necessariamente satisfaz a equação${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle \ zeta {\ big (} u, v {\ big)}}$

${\ displaystyle \ zeta {\ big (} u, v {\ big)} = au + bv + c}$

com constantes .${\ displaystyle a, b, c \ in \ mathbb {R}}$

A questão da generalização para dimensões superiores é conhecida como o problema de Bernstein e foi resolvida por Ennio de Giorgi , Enrico Bombieri e outros.

A partir deste teorema, o teorema de Liouville para superfícies mínimas segue imediatamente :

Uma solução da equação da área mínima não paramétrica que é limitada a uma completamente explicada cumpre o necessário${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle \ zeta {\ big (} u, v {\ big)}}$

${\ displaystyle \ zeta {\ big (} u, v {\ big)} = \ operatorname {const}}$.

Este é um análogo do teorema da teoria da função de Liouville .

A área de uma área mínima

A área de uma área mínima com a unidade normal é escrita no formulário ${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {n}}$

${\ displaystyle A = \ oint (\ mathbf {n}, \ mathbf {x}, \ mathrm {d} \ mathbf {x})}$.

Deve ser assumido que a curva limite é simplesmente fechada e continuamente diferenciável.

Fórmulas de representação

Para entender melhor as áreas mínimas, não basta considerar apenas as equações diferenciais que elas satisfazem, mas também encontrar representações especiais da solução.

Representação complexa

Apresentando os parâmetros isotérmicos uev, primeiro obtemos o sistema de superfície H para H = 0:

${\ displaystyle \ Delta \ mathbf {x} = 0, \ qquad \ mathbf {x} _ {u} ^ {2} - \ mathbf {x} _ {v} ^ {2} = 0 = \ mathbf {x} _ {u} \ mathbf {x} _ {v}}$

A equação de segunda ordem é, portanto, escrita na forma

${\ displaystyle {\ frac {\ partial ^ {2} \ mathbf {x}} {\ partial z ^ {1} \ partial z ^ {2}}} = 0}$

com as variáveis complexas e e ficamos com a representação ${\ displaystyle z ^ {1} = u + iv}$${\ displaystyle z ^ {2} = u-iv}$

${\ displaystyle 2 \ mathbf {x} = \ mathbf {y} (z ^ {1}) + \ mathbf {z} (z ^ {2}) \ qquad}$e .${\ displaystyle \ qquad (\ mathbf {y} ') ^ {2} = 0 = (\ mathbf {z}') ^ {2}, \ qquad \ mathbf {y} '\ mathbf {z}' \ neq 0 }$

Chamamos uma curva complexa que satisfaça as condições e uma curva isotrópica. Também chamamos uma área que pode ser escrito na forma de uma área de deslizamento .${\ displaystyle \ mathbf {y} (z)}$${\ displaystyle (\ mathbf {y} ') ^ {2} = 0}$${\ displaystyle \ mathbf {y} '\ neq 0}$${\ displaystyle \ mathbf {x} (u, v)}$${\ displaystyle \ mathbf {x} (u, v) = \ mathbf {y} (u) + \ mathbf {z} (v)}$

Uma definição generalizada de áreas mínimas é:

Uma superfície mínima é uma superfície deslizante cujos geradores são curvas isotrópicas.

As áreas mínimas reais atendem às condições

${\ displaystyle {\ overline {z ^ {1}}} = z ^ {2} \ qquad}$e .${\ displaystyle \ qquad \ mathbf {z} ({\ overline {z ^ {1}}}) = {\ overline {\ mathbf {y} (z_ {1})}}}$

Representação integral

A fórmula de representação em homenagem a Karl Weierstrass e Alfred Enneper fornece uma conexão entre a geometria diferencial e a teoria das funções . Ora, Weierstrass teve grande influência no desenvolvimento da teoria das funções. Essa fórmula de representação foi uma das razões pelas quais esse ramo relativamente novo da matemática foi levado a sério e teve tanto sucesso. Ele descobriu que toda superfície mínima não constante pode ser escrita como uma integral com as duas funções holomórficas ge h. O seguinte se aplica mais precisamente aos componentes: ${\ displaystyle \ mathbf {x} (w) = {\ big (} x (w), y (w), z (w) {\ big)}}$

${\ displaystyle x (w) = c_ {1} + \ operatorname {Re} \ int _ {w_ {0}} ^ {w} {\ frac {h (\ zeta) \ left (1-g (\ zeta) ^ {2} \ right)} {2}} \ mathrm {d} \ zeta}$,

${\ displaystyle y (w) = c_ {2} + \ operatorname {Re} \ int _ {w_ {0}} ^ {w} {\ frac {h (\ zeta) \ left (1 + g (\ zeta) ^ {2} \ right)} {2}} \ mathrm {d} \ zeta}$,

${\ displaystyle z (w) = c_ {3} + \ operatorname {Re} \ int _ {w_ {0}} ^ {w} h (\ zeta) g (\ zeta) \ mathrm {d} \ zeta}$

Esta fórmula de representação torna possível gerar imagens de qualquer superfície mínima com a ajuda de modernos sistemas de álgebra computacional. Por exemplo, algumas imagens de áreas mínimas neste artigo foram criadas usando essas fórmulas com o programa Maple .

Representação livre integral

Visto que vimos que, para integrar a equação diferencial H = 0, basta determinar as curvas isotrópicas, obtemos a chamada representação integral-livre para áreas mínimas reais.${\ displaystyle \ mathbf {x} (w) = {\ big (} x (w), y (w), z (w) {\ big)}}$

${\ displaystyle x (w) = \ operatorname {Re} \ left (\ pm i \ left (f (w) -wf '(w) - {\ frac {1-w ^ {2}} {2}} f '' (w) \ right) \ right)}$

${\ displaystyle y (w) = \ operatorname {Re} \ left (f (w) -wf '(w) + {\ frac {1 + w ^ {2}} {2}} f' '(w) \ direita)}$

${\ displaystyle z (w) = \ operatorname {Re} \ left (-i {\ big (} f '(w) -wf' '(w) {\ big)} \ right)}$

com uma função holomórfica que deve atender ao requisito. Os níveis, portanto, escapam a essa representação. A fim de esclarecer o significado das variáveis ​​complexas para uma área mínima real, fornecemos um cálculo demorado ${\ displaystyle f = f (w)}$${\ displaystyle f '' '\ neq 0}$${\ displaystyle w}$

${\ displaystyle w = {\ frac {n_ {1} + in_ {2}} {- 1 + n_ {3}}}}$ou ,${\ displaystyle {\ frac {1} {w}} = {\ frac {n_ {1} + in_ {2}} {- 1 + n_ {3}}}}$

aqui está o vetor normal unitário da área mínima. Resumimos: Especificando o número complexo ou o vetor normal da unidade da área mínima é determinado. Por outro lado, ou depende apenas . As afirmações nesta seção podem ser encontradas no livro Elementare Differentialgeometrie de W. Blaschke e K. Leichtweiß, consulte também a literatura . ${\ displaystyle \ mathbf {n} = (n_ {1}, n_ {2}, n_ {3})}$${\ displaystyle w}$${\ displaystyle 1 / w}$${\ displaystyle \ mathbf {n}}$${\ displaystyle w}$${\ displaystyle 1 / w}$${\ displaystyle \ mathbf {n}}$

Notas sobre a área funcional

Iremos primeiro derivar este funcional em geral e mostrar a invariância sob transformações de parâmetro orientadas positivamente . Finalmente, calcularemos explicitamente os casos especiais unidimensionais e bidimensionais.

Derivação e invariância de parâmetro

Notamos que nossa área mínima pode ser entendida como uma variedade m-dimensional no espaço vetorial real n-dimensional. Isso sempre é possível devido ao teorema de incorporação de Nash . Primeiro explicamos o tensor métrico

${\ displaystyle g_ {ij} (u): = {\ frac {\ partial \ mathbf {x} (u)} {\ partial u_ {i}}} {\ frac {\ partial \ mathbf {x} (u) } {\ u_ parcial {j}}}}$

com o determinante

${\ displaystyle g (u): = \ operatorname {det} (g_ {ij} (u)) _ {i, j = 1, \ dotsc, m}}$.

Lembramos que o conteúdo de uma área m-dimensional resulta como uma integral m-dimensional sobre a função característica dessa área. Uma função característica é identicamente uma em todas as partes do conjunto e, caso contrário, identicamente zero. Com isso, só precisamos expressar o elemento da interface do usuário de forma adequada. Explicamos os vetores tangentes em um ponto fixo u

${\ displaystyle {\ frac {\ partial \ mathbf {x} (u)} {\ partial u_ {i}}}}$ Pra ${\ displaystyle i, j = 1, \ dotsc, m}$

e escolher vetores de forma que o sistema ${\ displaystyle \ xi _ {m + 1}, \ dotsc, \ xi _ {n}}$

${\ displaystyle (\ mathbf {x} _ {u_ {1}}, \ dotsc, \ mathbf {x} _ {u_ {m}}, \ xi _ {m + 1}, \ dotsc, \ xi _ {n })}$

é orientado positivamente e preenche as duas condições e para todos os valores significativos de i e j. O elemento UI é assim escrito: ${\ displaystyle (\ mathbf {x} _ {u_ {i}}, \ xi _ {j}) = 0}$${\ displaystyle {\ big (} \ xi _ {i}, \ xi _ {j}) = \ delta _ {ij}}$

${\ displaystyle {\ begin {alinhados} \ mathrm {d} \ sigma (u) & = \ operatorname {det} (\ mathbf {x} _ {u_ {1}}, \ dotsc, \ mathbf {x} _ { u_ {m}}, \ xi _ {m + 1}, \ dotsc, \ xi _ {n}) \ mathrm {d} u_ {1} \ dotsm \ mathrm {d} u_ {m} \\ & = { \ sqrt {\ operatorname {det} ((\ mathbf {x} _ {u_ {1}}, \ dotsc, \ xi _ {n}) ^ {T} (\ mathbf {x} _ {u_ {1}} , \ dotsc, \ xi _ {n}))}} \ mathrm {d} u_ {1} \ dotsm \ mathrm {d} u_ {m} \\ & = {\ sqrt {\ operatorname {det} (g_ { ij} (u)) _ {i, j = 1, \ dotsc, m}}} ​​\ mathrm {d} u_ {1} \ dotsm \ mathrm {d} u_ {m} \\ & = {\ sqrt {g (u)}} \ mathrm {d} u_ {1} \ dotsm \ mathrm {d} u_ {m} \ end {alinhado}}}$

Para o determinante de duas matrizes com : ${\ displaystyle m \ times n}$${\ displaystyle m \ leq n}$

${\ displaystyle \ operatorname {det} (A ^ {T} B) = \ sum _ {1 \ leq i_ {1} <\ dotsb <i_ {m} \ leq n} \ operatorname {det} A_ {i_ {1 } \ dotso i_ {m}} \ operatorname {det} B_ {i_ {1} \ dotso i_ {m}}}$

Isto indica que a sub-matriz de que consiste somente das linhas . Com isso, podemos alterar o elemento da interface do usuário no formulário ${\ displaystyle A_ {i_ {1} \ dotso i_ {m}}}$${\ displaystyle A}$${\ displaystyle i_ {1}, \ dotsc, i_ {m}}$

${\ displaystyle \ mathrm {d} \ sigma (u) = {\ sqrt {\ sum _ {1 \ leq i_ {1} <\ dotsb <i_ {m} \ leq n} \ left ({\ frac {\ partial {\ big (} \ mathbf {x} _ {u_ {i_ {1}}}, \ dotsc, \ mathbf {x} _ {u_ {i_ {m}}} {\ big)}} {\ parcial {\ grande (} u_ {1}, \ dotsc, u_ {m} {\ big)}}} \ right) ^ {2}}} \ mathrm {d} u_ {1} \ dotsm \ mathrm {d} u_ {m }}$

Escreva. Com a ajuda da fórmula de transformação , determinamos agora a invariância sob as transformações de parâmetro de mesma direção do elemento de superfície e, portanto, da área funcional.

O conteúdo uni e bidimensional

Em uma dimensão espacial, este funcional é reduzido ao comprimento de caminho usual :

${\ displaystyle A (\ mathbf {x}) = \ int | \ mathbf {x} '(u) | \, \ mathrm {d} u}$

Se alguém tem uma superfície bidimensional que está embutida no espaço tridimensional, obtém-se com a identidade de Lagrange :

${\ displaystyle EG-F ^ {2} = | \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v} | ^ {2}}$

O seguinte se aplica à área funcional:

${\ displaystyle A (\ mathbf {x}) = \ iint | \ mathbf {x} _ {u} \ times \ mathbf {x} _ {v} | \, \ mathrm {d} u \ mathrm {d} v }$

literatura

• Wilhelm Blaschke , Kurt Leichtweiß: Geometria diferencial elementar (= ensinamentos básicos das ciências matemáticas. Volume 1). Springer-Verlag, 1973, online.
• Johannes CC Nitsche : Aulas sobre áreas mínimas (= ensinamentos básicos das ciências matemáticas. Volume 199). Springer-Verlag, 1975.
• David Gilbarg , Neil Trudinger : Equações diferenciais parciais elípticas de segunda ordem . Springer-Verlag, 1983.
• Ulrich Dierkes, Stefan Hildebrandt , Albrecht Küster, Ortwin Wohlrab: Superfícies mínimas (= ensinamentos básicos das ciências matemáticas. Volumes 295 e 296). Springer-Verlag, 1992, 2 volumes.
• Stefan Hildebrandt, Anthony Tromba: Esfera, círculo e bolhas de sabão, formas ideais na geometria e na natureza. Birkhäuser, 1996.
• Friedrich Sauvigny : Equações diferenciais parciais de geometria e física. Springer-Verlag, 2004 f., 2 volumes.

Links da web

• Eric W. Weisstein : Superfícies mínimas . In: MathWorld (inglês).
• Introdução gráfica às áreas mínimas
• Superfícies mínimas periódicas triplas
• 3D-XplorMath: Programa para Mac ou Java com muitas famílias de áreas mínimas

Evidência individual

1. ^ Superfícies mínimas , Mathworld
2. ^ Mathworld, superfície mínima de Henneberg