Geometria hiperbólica

Modelo de uma telha de um avião com quadrados. Mais de quatro encontram-se nas esquinas (dependendo do tamanho, aqui cinco).

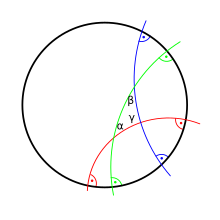
A geometria hiperbólica (também chamada de geometria Lobachevskiana ou geometria Lobachevsky ) é um exemplo de geometria não euclidiana que é obtida se adicionarmos o axioma hiperbólico contraditório aos axiomas da geometria absoluta em vez do axioma dos paralelos que caracteriza as geometrias euclidianas . Isso significa que para uma linha reta ge um ponto P (que não está em g ) não há apenas uma linha reta, como na geometria euclidiana, mas pelo menos duas linhas retas ( h e i ) que ir através P e são paralelas ao g . O facto de que duas linhas rectas são “paralelo” para um outro apenas meios que se encontram no mesmo plano e não têm pontos em comum, não que eles têm a mesma distância em toda a parte ( H e I têm apenas um ponto P em comum ).

Pode-se mostrar que, para qualquer linha reta g através de qualquer ponto fora de g, há infinitas linhas que não se cruzam (“paralelas”) que estão no plano definido pelo ponto e pela linha. Duas delas estão em uma posição limítrofe e são chamadas de borda- paralela (também: horoparalela) à linha reta, enquanto as linhas retas restantes são chamadas de superparalelas (também: hiperparalelas).

Representações do plano hiperbólico real

Existem diferentes maneiras pelas quais o plano hiperbólico real pode ser representado no plano euclidiano real. A maioria deles pode ser generalizada para dimensões superiores.

Em cada uma dessas maneiras, a mesma geometria hiperbólica abstrata é representada: o plano hiperbólico real. Portanto, é possível converter entre essas representações e afirmações em geometria puramente hiperbólica independentemente do "modelo" usado. Normalmente, fala-se de modelos diferentes em matemática quando duas estruturas não isomórficas satisfazem o mesmo sistema de axiomas. A este respeito, os seguintes “modelos” descrevem a mesma estrutura, portanto, são apenas representações diferentes de um modelo. No entanto, essas representações são sempre referidas como modelos na literatura , inclusive aqui. Para planos hiperbólicos sobre outros corpos e mais de espaços hiperbólicos bidimensionais, consulte Geometria absoluta métrica .

Modelo de disco circular de Beltrami e Klein

Nesta representação desenvolvida por Eugenio Beltrami e Felix Klein , aplica-se o seguinte:

• O plano hiperbólico é modelado por um disco circular aberto .
• Linhas hiperbólicas são modeladas por tendões .
• Os comprimentos são definidos por uma função de distância especial (os ângulos também são diferentes dos valores euclidianos).

Esta representação também é conhecida pelo nome de "geometria da esteira de cerveja".

Função distância

Distância entre dois pontos em uma geometria hiperbólica

São um e B , dois pontos do disco circular, de modo que por encontra Um e B acorde o círculo em dois pontos que se estende R e S . A distância hiperbólica entre A e B agora é definida usando a razão dupla : ${\ displaystyle (A, B, R, S)}$

${\ displaystyle d (A, B) = {\ frac {1} {2}} \ ln (A, B, R, S) = {\ frac {1} {2}} \ ln {\ frac {{\ overline {RB}} \ cdot {\ overline {SA}}} {{\ overline {RA}} \ cdot {\ overline {SB}}}}}$.

Modelo de disco circular de Poincaré

O seguinte se aplica ao modelo de disco circular de Henri Poincaré , que remonta a Beltrami :

• O plano hiperbólico é modelado por um disco circular aberto (geralmente o círculo unitário).
• As linhas retas hiperbólicas são modeladas por arcos (e diâmetros ) que são perpendiculares à aresta.
• A medição do ângulo hiperbólico corresponde à medição do ângulo euclidiano, sendo o ângulo entre dois arcos determinado por suas tangentes no ponto de intersecção.
• A medição do comprimento hiperbólico é realizada usando uma função especial de distância.

Função distância

Deixe e seja dois pontos do disco circular. Resumindo o plano como plano complexo, de modo que correspondem aos pontos , números complexos , . A distância hiperbólica de e agora é definida usando estes números complexos: ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle A}$${\ displaystyle B}$

${\ displaystyle d (A, B) = \ operatorname {arcosh} \ left (1 + {\ frac {2 \ cdot \ left \ | ab \ right \ | ^ {2}} {\ left (1- \ left \ | a \ right \ | ^ {2} \ right) \ cdot \ left (1- \ left \ | b \ right \ | ^ {2} \ right)}} \ right)}$

Modelo de meio plano de Poincaré

No modelo do meio plano de Henri Poincaré, que remonta a Beltrami:

• O plano hiperbólico é modelado pela metade superior do plano (y> 0).
• As linhas retas hiperbólicas são modeladas por arcos (e meias-linhas ) que são perpendiculares ao eixo x.
• A medição do ângulo hiperbólico corresponde à medição do ângulo euclidiano, em que o ângulo entre dois arcos circulares é determinado por meio de suas tangentes no ponto de intersecção.

Função distância

A distância entre dois pontos do semiplano superior é calculada usando a seguinte fórmula:

${\ displaystyle \ operatorname {d} (\ langle x_ {1}, y_ {1} \ rangle, \ langle x_ {2}, y_ {2} \ rangle) = \ operatorname {arcosh} \ left (1 + {\ frac {{(x_ {2} -x_ {1})} ^ {2} + {(y_ {2} -y_ {1})} ^ {2}} {2y_ {1} y_ {2}}} \ certo) \ ,.}$

Modelo hiperbolóide

O modelo hiperbólico, que remonta a Poincaré, incorpora o plano hiperbólico no espaço tridimensional de Minkowski .

Programa Erlangen

No sentido do programa Erlanger de Felix Klein , geometria hiperbólica é a geometria de

${\ displaystyle (O (n, 1), O (n) \ vezes O (1))}$.

O modelo Beltrami-Klein mostra que a geometria hiperbólica pode ser entendida como parte da geometria projetiva.

triângulo

Triângulo no espaço hiperbólico

Na geometria hiperbólica real, a soma dos ângulos em um triângulo é sempre menor do que π (180 graus; ou dois direitos, se você quiser evitar a medida do ângulo). Para triângulos muito grandes, pode ser feito tão pequeno quanto você quiser. A área do triângulo é calculada usando a fórmula de Johann Heinrich Lambert :

${\ displaystyle \ pi - (\ alpha + \ beta + \ gamma) = C \, \ Delta,}$

onde α , β e γ são os respectivos ângulos, Δ é a área e a constante C é um fator de escala. O fator de escala C depende do sistema de unidades usado e deve ser basicamente definido como 1. Se o fator C for negativo, fala-se de uma curvatura gaussiana (positiva) . Da mesma forma, Thomas Harriot definiu anteriormente a fórmula em 1603

${\ displaystyle \ Delta = R ^ {2} \, (\ alpha + \ beta + \ gamma - \ pi)}$

para a área de um triângulo em uma superfície esférica que é formada por círculos com o mesmo raio da esfera. O relacionamento se aplica aqui

${\ displaystyle C = - {\ frac {1} {R ^ {2}}}}$.

Uma vez que a geometria hiperbólica requer um valor positivo para C , R deve ser devido a

${\ displaystyle R = (- C) ^ {- {\ frac {1} {2}}}}$

agir em torno de um raio imaginário .

Veja também

• Espaço hiperbólico
• Geometria elíptica
• Nikolai Lobachevsky
• János Bolyai
• Giovanni Girolamo Saccheri e Saccheri-Viereck

literatura

história

• Jeremy Gray: Idéias de Espaço: Euclidiana, Não-Euclidiana e Relativística . 2ª Edição. Oxford University Press, Oxford 1989, ISBN 0-19-853935-5 . 
• Marvin Jay Greenberg: Geometrias Euclidiana e Não Euclidiana: Desenvolvimento e História. WH Freeman, 1993, ISBN 0-7167-2446-4 .
• David Hilbert : Fundamentals of Geometry . 14ª edição. Teubner, Stuttgart / Leipzig 1999, ISBN 3-519-00237-X ( cópia online da edição de 1903 [acesso em 28 de junho de 2013]). 
• Nikolai I. Lobachevsky: Pangeometria, editado e traduzido por Athanase Papadopoulos, Heritage of European Mathematics. Vol. 4, European Mathematical Society (EMS), Zurique, ISBN 978-3-03719-087-6 .

A geometria hiperbólica no contexto da geometria diferencial (geometrias em superfícies)

• Norbert A'Campo, Athanase Papadopoulos: Notas sobre geometria hiperbólica. In: Estrasburgo Master class on Geometry. European Mathematical Society (EMS), Zurich, ISBN 978-3-03719-105-7 , pp. 1-182, doi: 10.4171 / 105 . (IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18)
• Athanase Papadopoulos (Ed.): Manual da teoria de Teichmüller. Vol. I, European Mathematical Society (EMS), Zurich 2007, ISBN 978-3-03719-029-6 , doi: 10.4171 / 029 . (IRMA Aulas de Matemática e Física Teórica 11)
• Athanase Papadopoulos (Ed.): Manual da teoria de Teichmüller. Vol. II, European Mathematical Society (EMS), Zurich 2009, ISBN 978-3-03719-055-5 , doi: 10.4171 / 055 . (IRMA Aulas de Matemática e Física Teórica 13)
• Athanase Papadopoulos (Ed.): Manual da teoria de Teichmüller. Vol. III, European Mathematical Society (EMS), Zurique 2012, ISBN 978-3-03719-103-3 , doi: 10.4171 / 103 . (IRMA Aulas de Matemática e Física Teórica 19)

O plano (real) hiperbólico como modelo de uma geometria absoluta no sentido hilbertiano

• Friedrich Bachmann : Estrutura da geometria a partir do conceito de reflexão . 2ª edição complementada. Springer, Berlin / Heidelberg / New York 1973, ISBN 3-540-06136-3 , V: Hyperbolic Geometry and §20.13: Hilbert Planes ( define geometria absoluta de forma muito geral, explica as características especiais da geometria hiperbólica real contra este pano de fundo). 
• Benno Klotzek: geometrias elementares euclidianas e não euclidianas . 1ª edição. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0 ( elementar não significa simplesmente aqui : resolver tarefas de construção e coordenar as geometrias não euclidianas “clássicas”). 

Evidência individual

1. ↑ ^{a b} Klotzek (2001), 2.1
2. ↑ Susanne Müller-Philipp, Hans-Joachim Gorski: Guia de geometria: para alunos de postos de ensino . Vieweg + Teubner Verlag, 5ª edição expandida, 2012, ISBN 978-3-8348-1234-6 , p. 71 ( trecho (Google) )