Polígono

Diferentes concepções de polígonos e áreas poligonais

Um polígono (do grego antigo πολυγώνιον polygṓnion 'polígono'; de πολύς polýs 'much' e γωνία gōnía 'ângulo') ou polígono é uma figura geométrica plana na geometria elementar que é formada por uma linha fechada .

Um polígono é um politopo bidimensional .

Um polígono é obtido por (não colinear) em um plano pelo menos três pontos diferentes por estiramento são ligados entre si. Isso cria uma linha fechada ( polígono ) com tantos cantos , por exemplo, um triângulo (3 pontos, 3 linhas) ou um quadrado (4 pontos, 4 linhas).

A área fechada costuma ser chamada de polígono, como na planimetria .

Definição e termos

Um polígono é uma figura definida por uma tupla de diferentes pontos. ${\ displaystyle P: = \ left (P_ {1}, P_ {2}, \ dotsc, P_ {n} \ right), P_ {i} \ in \ mathbb {R} ^ {2}, 1 \ leq i \ leq n}$${\ displaystyle n}$

• Os pontos são chamados de cantos ou cantos do polígono, para abreviar , um polígono com cantos é chamado -Eck ou (especialmente na literatura inglesa) também -on.${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$
• As linhas e são chamadas de lados do polígono.${\ displaystyle {\ overline {P_ {i} P_ {i + 1}}} \ left (i = 1, \ dotsc, n-1 \ right)}$${\ displaystyle {\ overline {P_ {n} P_ {1}}}}$
• Todas as linhas de conexão entre dois pontos de canto que não são lados são chamadas diagonais .

Às vezes, outras condições são necessárias para a definição de um polígono, mas não são formalmente necessárias:

• Um polígono tem pelo menos três pontos de vértice que diferem uns dos outros em pares. Isso exclui um "triângulo duplo".
• Três pontos de canto adjacentes não estão em uma linha reta. Além disso , , e , , irá ser considerado como vértices adjacentes. Isso exclui cantos com ângulos retos.${\ displaystyle P_ {n}}$${\ displaystyle P_ {1}}$${\ displaystyle P_ {2}}$${\ displaystyle P_ {n-1}}$${\ displaystyle P_ {n}}$${\ displaystyle P_ {1}}$

classificação

Ilustração histórica de polígonos (1699)

Por número de cantos

Os polígonos são normalmente nomeados de acordo com o número de cantos (peso do polígono).

Polígono regular

Se um polígono tem os mesmos lados e os mesmos ângulos internos, ele é chamado de polígono regular ou polígono regular. Muitos polígonos regulares podem ser construídos com bússolas e réguas ( polígonos construtíveis ).

Lista de polígonos regulares

Cantos	Descrição	grego	Bússola + régua	Especialidade
1	Um canto	Monogônico	-	Apontar
2	Delta	Digon	-	rota
3	triângulo	Trine	sim	1. Número primo de Fermat ${\ displaystyle 3 = 2 ^ {2 ^ {0}} + 1}$
4º	quadrado	Tetragon	sim	quadrado
5	Pentágono	Pentágono	sim	2. Número primo de Fermat ${\ displaystyle 5 = 2 ^ {2 ^ {1}} + 1}$
6º	hexágono	hexágono	sim
7º	heptágono	heptágono	não	Possível construção aproximada, heptágono de acordo com Arquimedes
8º	octógono	Octógono	sim	inglês de outubro a gon
9	Neuneck	Nonagon	não	Eneagono raro , construção de aproximação possível
10	decágono	Decágono	sim
11	Duende	Hendekagon	não	Possível construção aproximada
12º	Dodecágono	Dodecágono	sim
13	Triângulo	Tridecágono	não
14º	Quatorze	Tetradecágono	não
Dia 15	Décimo quinto	Pentadecágono	sim
16	Hexágono	Hexadecágono	sim
Dia 17	Décima sétima curva	Heptadecágono	sim	3. Número primo de Fermat ${\ displaystyle 17 = 2 ^ {2 ^ {2}} + 1}$
18º	Décimo oitavo	Octodecágono	não	inglês oct a decagon, octakaidecagon
19º	Décimo nono	Nonadekagon	não	Inglês também eneadecágono , eneakaidecagon
20o	Vigésimo	Ikosagon	sim
21	Vinte e um	Ikosihenagon	não
24	Vinte e quatro quadrados	Icositetragon	sim
30º	Canto trinta e quatro	Triakontagon	sim
40	Tetragonal	Tetracontágono	sim
50	Cinquenta pontos	Pentacontágono	não
51	Cinquenta e um	Pentacontahenagon	sim
60	Hexágono	Contato hexágono	sim
70	Septuagésimo	Heptakontagon	não
80	Octogonal	Octocontagon	sim	Inglês outubro um contagon
85	Oitenta e cinco quadrados	Octocontapentágono	sim	Inglês outubro um contapentagon
90	Noventa e quatro	Enneakontagon	não
100	Hunderteck	Hectogon	não
257	Canto 257		sim	4. Número primo de Fermat ${\ displaystyle 257 = 2 ^ {2 ^ {3}} + 1}$
1.000	Milhares de peças	Chiliagon
10.000	Dezenas de milhares	Myriagon
65.537	Canto 65537		sim	5. Número primo de Fermat ${\ displaystyle 65.537 = 2 ^ {2 ^ {4}} + 1}$
100.000	Centenas de milhares
1.000.000	Canto 1000000	Megagon
4.294.967.295	4294967295 canto		sim	O maior número ímpar de cantos conhecido que pode teoricamente ser construído com uma bússola e régua
${\ displaystyle 10 ^ {100}}$	Googoleck	Googolgon		Número do canto: a 1 com 100 zeros
∞	Canto infinito	Apeirogon		Forma de limite teórico com um número infinito de lados

Mais tipos

Classificação de polígonos

Polígono virado

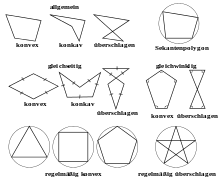
Se as bordas se cruzam (se tocam) não apenas nos pontos dos cantos, o polígono é denominado capotamento . Se não houver autointerseção, o polígono é denominado simples .

Polígono não revirado

Os polígonos que não são invertidos podem ser convexos (todos os ângulos internos são menores que 180 °) ou não convexos (pelo menos um ângulo interno é maior que 180 °).

Polígono plano

No polígono plano (planar).

Polígono não plano

Polígono no espaço (não plano).

Os polígonos podem ser equiláteros ou equiangulares :

Polígono regular

Se um polígono tiver os mesmos lados e os mesmos ângulos internos, ele será chamado de polígono regular ou polígono regular.

Polígono estrela

Polígonos regulares invertidos planares também são conhecidos como polígonos em estrela devido à sua aparência .

Polígono ortogonal

Com polígonos ortogonais, todas as arestas se encontram em ângulos retos (ou seja, o ângulo interno é de 90 ° ou 270 ° em cada aresta).

propriedades

ângulo

Em um canto plano que não está virado está a soma dos ângulos internos${\ displaystyle n}$

${\ displaystyle \ alpha _ {1} + \ dotsb + \ alpha _ {n} = (n-2) \ cdot 180 ^ {\ circ}}$.

O seguinte então se aplica à soma dos ângulos externos, independentemente do número de cantos

${\ displaystyle \ alpha _ {1} '+ \ dotsb + \ alpha _ {n}' = 360 ^ {\ circ}}$.

Além disso, se todos os ângulos internos e externos forem iguais, eles terão o valor

${\ displaystyle \ alpha = {\ frac {(n-2)} {n}} \ cdot 180 ^ {\ circ}}$   ou   .${\ displaystyle \ alpha '= {\ frac {1} {n}} \ cdot 360 ^ {\ circ}}$

Diagonais

Para polígonos que não são cruzados, as seguintes considerações se aplicam ao calcular o número de diagonais:

1. Cada um dos cantos pode ser conectado a um dos outros cantos por um link.${\ displaystyle n}$
2. A conexão de canto a canto é idêntica à conexão de para .${\ displaystyle P_ {a}}$${\ displaystyle P_ {b}}$${\ displaystyle P_ {b}}$${\ displaystyle P_ {a}}$
3. Exatamente as conexões são lados do polígono.${\ displaystyle n}$

Portanto, um canto que não está virado tem exatamente diagonais. No caso de um polígono não convexo, existem diagonais fora do polígono (na área de um ângulo interno truncado). ${\ displaystyle n}$${\ displaystyle {\ tfrac {n \ cdot (n-1)} {2}} - n = {\ tfrac {n \ cdot (n-3)} {2}}}$

alcance

Se os pontos de canto de um polígono plano simples são dados por coordenadas cartesianas , o perímetro do polígono pode ser determinado adicionando os comprimentos laterais calculados usando o teorema de Pitágoras : ${\ displaystyle (x_ {i}, y_ {i})}$

${\ displaystyle \ mathrm {U} \ = \ {\ sqrt {(x_ {1} -x_ {n}) ^ {2} + (y_ {1} -y_ {n}) ^ {2}}} \ + \ \ sum _ {i = 1} ^ {n-1} {\ sqrt {(x_ {i + 1} -x_ {i}) ^ {2} + (y_ {i + 1} -y_ {i}) ^ {2}}}}$

área

Se os pontos de canto de um polígono plano simples são dados por coordenadas cartesianas , a área do polígono pode ser calculada de acordo com a fórmula trapezoidal gaussiana : ${\ displaystyle (x_ {i}, y_ {i})}$

${\ displaystyle \ mathrm {2} A \ = \ \ left | \ sum _ {i = 1} ^ {n} (y_ {i} + y_ {i + 1}) \ cdot (x_ {i} -x_ { i + 1}) \ right | \ = \ \ left | \ sum _ {i = 1} ^ {n} (x_ {i} + x_ {i + 1}) \ cdot (y_ {i + 1} -y_ {i}) \ right | \ = \ \ left | \ sum _ {i = 1} ^ {n} (x_ {i} \ cdot y_ {i + 1} -y_ {i} \ cdot x_ {i + 1 }) \ right |}$.

Aqui, os índices maiores do que sempre são considerados módulo , ou seja , o que se entende por: ${\ displaystyle n}$ ${\ displaystyle n}$${\ displaystyle x_ {n + 1}}$${\ displaystyle x_ {1}}$

${\ displaystyle 2A \ = \ \ left | x_ {n} \ cdot y_ {1} -y_ {n} \ cdot x_ {1} + \ sum _ {i = 1} ^ {n-1} (x_ {i } \ cdot y_ {i + 1} -y_ {i} \ cdot x_ {i + 1}) \ right |}$

Na forma determinante, a fórmula trapezoidal gaussiana é:

${\ displaystyle 2A \ = \ \ left | \ quad {\ begin {vmatrix} x_ {n} & y_ {n} \\ x_ {1} & y_ {1} \ end {vmatrix}} + \ sum _ {i = 1} ^ {n-1} {\ begin {vmatrix} x_ {i} & y_ {i} \\ x_ {i + 1} & y_ {i + 1} \ end {vmatrix}} \ quad \ right | }$

Além da fórmula trapezoidal gaussiana, a área de um polígono pode ser calculada usando uma soma assinada das áreas dos triângulos que são formados com as bordas do polígono como base e um ponto fixo (por exemplo, o ponto de origem ) como o ápice. As áreas dos triângulos com a base voltada para longe do ponto fixo (como a borda do polígono) recebem um sinal negativo.

A área de polígonos de rede cujos cantos estão todos em uma rede pode ser calculada com o teorema de Pick .

Algoritmos

Área

Especialmente para a programação, a seguinte representação é a fórmula trapezoidal gaussiana particularmente adequada porque para salvar as matrizes de coordenadas, a indexação de matrizes em muitas linguagens de programação começa já do zero e a função módulo pode, portanto, ser usada de maneira elegante. A função módulo é necessária aqui para excluir os chamados erros off-by-one na indexação da matriz. Aqui, , , , as coordenadas dos vértices do polígono. ${\ displaystyle (x_ {i}, y_ {i})}$${\ displaystyle i = 0 \ dotsc n-1}$${\ displaystyle n \ in \ mathbb {N}}$${\ displaystyle n \ geq 3}$

${\ displaystyle A = {\ frac {1} {2}} \ left | \ sum _ {i = 0} ^ {n-1} (y_ {i} + y_ {i + 1 {\ bmod {n}} }) (x_ {i} -x_ {i + 1 {\ bmod {n}}}) \ right |}$

O seguinte código de programa tem como objetivo mostrar uma implementação exemplar - aqui na linguagem de programação C # :

public double berechnePolygonFlaeche(double[] x, double[] y)
{
    if ((x == null) || (y == null)) // auf leere Argumente testen
    {
        return 0.0;
    }
    int anzahlDerEcken = Math.Min(x.Length, y.Length);
    if (anzahlDerEcken < 3) // ein Polygon hat mindestens drei Eckpunkte
    {
        return 0.0;
    }
    double flaecheninhalt = 0.0;
    
    // Schleife zwecks Summenbildung
    for (int i = 0; i < anzahlDerEcken; i++)
    {
        // Modulo-Funktion für die Indexe der Koordinaten
        flaecheninhalt += (y[i] + y[(i + 1) % anzahlDerEcken]) * (x[i] - x[(i + 1) % anzahlDerEcken]);
    }
    return Math.Abs(flaecheninhalt / 2.0);
}

As coordenadas dos pontos de canto são armazenados nas duas matrizes x e y. Para o pentágono de exemplo , que tem uma área de 45, essas matrizes podem, e. B. inicializado da seguinte forma:${\ displaystyle ((7.0), (8.7), (4.9), (1.6), (1.2))}$

double[] x = {7.0, 8.0, 4.0, 1.0, 1.0}; // beispielhafte x-Koordinaten des Polygons
double[] y = {0.0, 7.0, 9.0, 6.0, 2.0}; // beispielhafte y-Koordinaten des Polygons

Casco convexo

Casco convexo de pontos no avião

Algoritmos para a determinação do casco convexo de pontos no plano têm como limite inferior um tempo de execução assintótico de . A prova é feita reduzindo-a à classificação de números (ver procedimento de classificação ). Se apenas os pontos estiverem na borda do casco convexo, o limite será incluído . ${\ displaystyle n}$ ${\ displaystyle \ Omega (n \ log n)}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle \ Omega (n \ log k)}$

Existem vários algoritmos para determinar o casco convexo :

• Algoritmo de varredura de Graham
• Algoritmo de envoltura de veneno
• QuickHull
• Algoritmo incremental
• Algoritmo de Chan

Ponto no polígono

O número de cruzamentos do raio com as bordas indica se o ponto é dentro ou fora do polígono.

Existe um algoritmo simples que pode ser usado para verificar se um ponto está dentro de um polígono no plano :

Um raio horizontal é colocado através do ponto que está sendo examinado e com que freqüência o raio cruza as bordas do polígono. O ponto está dentro do polígono se o número de pontos de interseção à direita do ponto for ímpar. Se o número for par, o ponto está fora.

O seguinte programa de computador na linguagem de programação C # mostra uma possível implementação:

// Bestimmt, ob sich ein Punkt mit den Koordinaten (x, y) innerhalb des Polygons befindet
public bool PunktIstInnerhalb(PointF[] ecken, int x, int y)
{
	int anzahlDerSchnittpunkte = 0;
	int anzahlDerEcken = ecken.Length;
	
	// Ermittelt die Anzahl der Schnittpunkte des Strahls mit den Kanten des Polygons
	for (int i = 0; i < anzahlDerEcken; i++)
	{
		// Die Ecken der untersuchten Kante
		PointF ecke1 = ecken[i];
		PointF ecke2 = ecken[(i + 1) % anzahlDerEcken];
		double x1 = ecke1.X;
		double y1 = ecke1.Y;
		double x2 = ecke2.X;
		double y2 = ecke2.Y;
		
		// Prüft, ob der Strahl die Kante des Polygons schneidet
		if (x < x1 && x > x2 || x > x1 && x < x2 && y > (x * y1 - x * y2 - x2 * y1 + x1 * y2) / (x1 - x2))
		{
			anzahlDerSchnittpunkte++;
		}
	}
	// Wenn die Anzahl ungerade ist, gib true zurück
	// Wenn die Anzahl gerade ist, gib false zurück
	return anzahlDerSchnittpunkte % 2 == 1; // Modulo-Operation für Division durch 2
}

usar

Na ciência da computação , aproximações importantes de polígonos complexos são o casco convexo e o retângulo minimamente circundante . Em algoritmos, uma possível interseção não vazia com outro objeto geométrico é frequentemente testada primeiro (ou isso é excluído) com base na aproximação, somente então o polígono inteiro é carregado na memória e uma interseção exata é calculada.

Na computação gráfica 3D , além de outros métodos de modelagem geométrica, quaisquer superfícies (incluindo curvas) são modeladas como uma malha poligonal . As malhas triangulares são particularmente adequadas para a exibição rápida de superfícies, mas também não podem ser interpoladas usando superfícies de subdivisão . Existem várias estruturas de dados conhecidas para armazenar redes poligonais.

Polígonos regulares são freqüentemente usados ​​como planta baixa em arquitetura. Exemplos conhecidos:

• 05-Eck : Pentágono em Arlington, Virgínia
• 0Octógono : Castel del Monte em Apúlia, Itália
• 12 esquinas : Saarpolygon , memorial da mineração de carvão em Ensdorf (Saar), Saarland
• 16 esquinas : farol Huisduinen perto de Den Helder, Holanda
• Esquina 18: Liberation Hall em Kelheim, Baviera
• Esquina 30: Wiener Riesenrad em Viena, Áustria

Exemplos de polígonos em engenharia mecânica

Além disso, o termo polígono também é usado analogamente para uso como uma conexão eixo-cubo poligonal de travamento positivo em engenharia mecânica. Quaisquer perfis poligonais são concebíveis aqui.

Exemplos de polígonos em geografia

Estados dos EUA com contornos poligonais

Cada uma das fronteiras dos estados americanos de Colorado e Wyoming faz fronteira com um retângulo e, portanto, com um polígono convexo.

Os estados do Novo México e Utah têm cada um a forma de um polígono côncavo.

Veja também

• Polígono construtível
• poliedro

Links da web

Wikcionário: Polígono  - explicações de significados, origens das palavras, sinônimos, traduções

Wikcionário: Polígono  - explicações de significados, origens das palavras, sinônimos, traduções

• Eric W. Weisstein : Polygon . In: MathWorld (inglês).
• Para a matemática de polígonos irregulares
• Cálculo online de polígonos planos com saída gráfica

Evidência individual

1. ^ Wilhelm Gemoll : escola grego-alemão e dicionário manual . G. Freytag Verlag / Hölder-Pichler-Tempsky, Munique / Viena 1965. 
2. ↑ Cha Zhang, Tsuhan Chen: Extração eficiente de recursos para objetos 2D / 3D em representação de malha (PDF; 66 kB). Processamento de imagem, 2001. Proceedings. Conferência Internacional de 2001 sobre. Vol. 3. IEEE, 2001. APA (Inglês).
3. ↑ GeeksforGeeks: Como verificar se um determinado ponto está dentro ou fora de um polígono?