Ilustração linear

Reflexão de eixo como exemplo de mapeamento linear

Um mapeamento linear (também chamado de transformação linear ou homomorfismo do espaço vetorial ) é um tipo importante de mapeamento entre dois espaços vetoriais no mesmo campo na álgebra linear . No caso de um mapeamento linear, é irrelevante se você adiciona dois vetores primeiro e depois mapeia sua soma ou mapeia os vetores primeiro e depois adiciona a soma das imagens. O mesmo se aplica à multiplicação com um escalar do corpo básico.

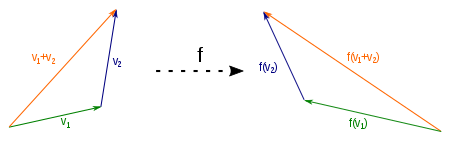
O exemplo mostrado de uma reflexão no eixo Y ilustra isso. O vector é a soma dos vetores e e sua imagem é o vetor . Mas você também consegue se adicionar as imagens e os vetores e . ${\ displaystyle c}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle {c '}}$${\ displaystyle {c '}}$${\ displaystyle {a '}}$${\ displaystyle {b '}}$${\ displaystyle a}$${\ displaystyle b}$

Diz-se então que um mapeamento linear é compatível com as combinações de adição vetorial e multiplicação escalar . O mapeamento linear é, portanto, um homomorfismo (mapeamento com preservação de estrutura) entre espaços vetoriais.

Na análise funcional , ao considerar espaços vetoriais de dimensão infinita que carregam uma topologia , geralmente se fala de operadores lineares em vez de mapeamentos lineares. Do ponto de vista formal, os termos são sinônimos. No caso de espaços vetoriais de dimensão infinita, no entanto, a questão da continuidade é significativa, enquanto a continuidade está sempre presente em mapeamentos lineares entre espaços vetoriais reais de dimensão finita (cada um com a norma euclidiana ) ou, mais geralmente, entre espaços vetoriais topológicos de Hausdorff de dimensão finita .

definição

Ser e espaços vetoriais sobre um corpo básico comum . Um mapeamento é chamado de mapeamento linear se todas e as seguintes condições se aplicarem: ${\ displaystyle V}$${\ displaystyle W}$ ${\ displaystyle K}$${\ displaystyle f \ dois pontos V \ a W}$${\ displaystyle x, y \ in V}$${\ displaystyle a \ in K}$

• ${\ displaystyle f}$ é homogêneo:

  ${\ displaystyle f \ left (ax \ right) = af \ left (x \ right)}$

• ${\ displaystyle f}$ é aditivo:

  ${\ displaystyle f \ left (x + y \ right) = f \ left (x \ right) + f \ left (y \ right)}$

As duas condições acima também podem ser resumidas:

${\ displaystyle f \ left (ax + y \ right) = af \ left (x \ right) + f \ left (y \ right)}$

Para isso entra a condição para a homogeneidade e para a para a aditividade. Outra condição equivalente é o requisito de que o gráfico do mapeamento seja um subespaço da soma dos espaços vetoriais e . ${\ displaystyle y = 0_ {V}}$${\ displaystyle a = 1_ {K}}$${\ displaystyle f}$${\ displaystyle V}$${\ displaystyle W}$

Explicação

Um mapeamento é linear se for compatível com a estrutura do espaço vetorial. Em outras palavras: os mapeamentos lineares são compatíveis com a adição e multiplicação escalar subjacente do domínio de definição e valor. A compatibilidade com a adição significa que o mapeamento linear recebe somas. Se tivermos uma soma com na área de definição , então essa soma é válida e, portanto, permanece na área de valor conforme a ilustração: ${\ displaystyle f \ dois pontos V \ a W}$${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle v_ {1}, v_ {2}, v_ {3} \ in V}$${\ displaystyle f (v_ {3}) = f (v_ {1}) + f (v_ {2})}$

${\ displaystyle \ forall v_ {1}, v_ {2}, v_ {3} \ in V {\ Big (} v_ {3} = v_ {1} + v_ {2} \ implica f (v_ {3}) = f (v_ {1}) + f (v_ {2}) {\ Big)}}$

Essa implicação pode ser abreviada colocando a premissa em . É assim que você recebe a demanda . A compatibilidade com a multiplicação escalar pode ser descrita de forma análoga. Isso é cumprido se resultar da conexão com o escalar e na faixa de definição que o seguinte também se aplica à faixa de valores: ${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle f (v_ {3}) = f (v_ {1}) + f (v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2}) = f (v_ {1}) + f (v_ {2})}$${\ displaystyle {\ tilde {v}} = \ lambda v}$${\ displaystyle \ lambda \ in K}$${\ displaystyle v \ in V}$${\ displaystyle f ({\ tilde {v}}) = \ lambda f (v)}$

${\ displaystyle \ forall {\ tilde {v}}, v \ in V \, \ forall \ lambda \ in K {\ Big (} {\ tilde {v}} = \ lambda v \ implica f ({\ tilde { v}}) = \ lambda f (v) {\ Big)}}$

Após inserir a premissa na conclusão , recebe-se a demanda . ${\ displaystyle {\ tilde {v}} = \ lambda v}$${\ displaystyle f ({\ tilde {v}}) = \ lambda f (v)}$${\ displaystyle f (\ lambda v) = \ lambda f (v)}$

• 

  A visualização da compatibilidade com a adição de vectores: Cada triângulo disso dado por , e é retido pelo mapeamento linear . Além disso , e forma um triângulo de adição e se aplica . ${\ displaystyle v_ {1}}$${\ displaystyle v_ {2}}$${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle f}$${\ displaystyle f (v_ {1})}$${\ displaystyle f (v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2}) = f (v_ {1}) + f (v_ {2})}$

• 

  Para mapeamentos que não são compatíveis com adição, existem vetores , e , portanto , e não formam um triângulo de adição porque é. Esse mapeamento não é linear. ${\ displaystyle v_ {1}}$${\ displaystyle v_ {2}}$${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle f (v_ {1})}$${\ displaystyle f (v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2}) \ neq f (v_ {1}) + f (v_ {2})}$

• 

  Visualização da compatibilidade com multiplicação escalar: Cada escala é mantida por um mapeamento linear e se aplica . ${\ displaystyle \ lambda v}$${\ displaystyle f (\ lambda v) = \ lambda f (v)}$

• 

  Se um mapeamento não for compatível com a multiplicação escalar, há um escalar e um vetor para que a escala não seja mapeada na escala . Esse mapeamento não é linear. ${\ displaystyle \ lambda}$${\ displaystyle v}$${\ displaystyle \ lambda v}$${\ displaystyle \ lambda f (v)}$

Exemplos

• Para cada mapeamento linear tem a forma com .${\ displaystyle V = W = \ mathbb {R}}$${\ displaystyle f (x) = mx}$${\ displaystyle m \ in \ mathbb {R}}$
• É e . Em seguida, um mapeamento linear é definido para cada matriz com a ajuda da multiplicação de matrizes . Qualquer mapeamento linear de a pode ser representado dessa maneira.${\ displaystyle V = \ mathbb {R} ^ {n}}$${\ displaystyle W = \ mathbb {R} ^ {m}}$${\ displaystyle m \ times n}$${\ displaystyle A}$
  ${\ displaystyle f \ colon \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {m}}$
  
  ${\ displaystyle f (x) = A \, x = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1n} \\\ vdots && \ vdots \\ a_ {m1} & \ dots & a_ {mn} \ end {pmatrix}} {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}}}$
  ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {m}}$
• É um intervalo aberto do espaço vectorial das funções continuamente diferenciáveis e o espaço vectorial das funções contínuas em , de modo que o quadro é , , a cada função atribui o seu derivado, linear. O mesmo se aplica a outros operadores diferenciais lineares .${\ displaystyle I \ subset \ mathbb {R}}$${\ displaystyle V = C ^ {1} (I, \ mathbb {R})}$${\ displaystyle \ mathbb {R}}$${\ displaystyle I}$${\ displaystyle W = C ^ {0} (I, \ mathbb {R})}$${\ displaystyle \ mathbb {R}}$${\ displaystyle I}$
  ${\ displaystyle D \ dois pontos C ^ {1} (I, \ mathbb {R}) \ para C ^ {0} (I, \ mathbb {R})}$${\ displaystyle f \ mapsto f '}$
  ${\ displaystyle f \ in C ^ {1} (I, \ mathbb {R})}$

• 

  O alongamento é um mapa linear. Nesta ilustração, o componente é alongado pelo fator . ${\ displaystyle f (x, y) = (2x, y)}$${\ displaystyle x}$${\ displaystyle 2}$

• 

  Este valor é aditivo: Não importa que apenas adicionando vetores e, em seguida, mapear ou se única mapeia os vetores e depois acrescentou: . ${\ displaystyle f (a + b) = f (a) + f (b)}$

• 

  Esta figura é homogênea: não importa se você só escalou um mapeamento vector e, em seguida, ou se únicos mapas e ajusta o vetor: . ${\ displaystyle f (\ lambda a) = \ lambda f (a)}$

Imagem e núcleo

Dois conjuntos de importância ao olhar para mapas lineares são a imagem e o núcleo de um mapa linear . ${\ displaystyle f \ dois pontos V \ a W}$

• A imagem da figura é o conjunto de vectores de imagem abaixo , isto é, o conjunto de todos com a . A quantidade de imagens, portanto, também é anotada por. A imagem é um subespaço de .${\ displaystyle \ mathrm {im} (f)}$${\ displaystyle f}$${\ displaystyle f (v)}$${\ displaystyle v}$${\ displaystyle V}$${\ displaystyle f (V)}$${\ displaystyle W}$

• O núcleo do mapeamento é o conjunto de vetores a partir dos quais são mapeados no vetor zero de by. É um subespaço de . O mapeamento é injetivo se e somente se o kernel contém apenas o vetor zero.${\ displaystyle \ mathrm {ker} (f)}$${\ displaystyle V}$${\ displaystyle f}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle f}$

características

• Um mapa linear entre espaços vetoriais e forma o vetor zero do vetor zero de: porque${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle W}$
  ${\ displaystyle f (0_ {V}) = 0_ {W}}$${\ displaystyle f \ left (0_ {V} \ right) = f \ left (0 \ cdot 0_ {V} \ right) = 0 \ cdot f \ left (0_ {V} \ right) = 0_ {W}. }$
• O teorema do homomorfismo descreve uma relação entre o núcleo e a imagem de um mapeamento linear : O fator espaço é isomórfico à imagem .${\ displaystyle f \ dois pontos V \ a W}$ ${\ displaystyle V / \ mathrm {ker} (f)}$${\ displaystyle \ mathrm {im} (f)}$

Mapeamentos lineares entre espaços vetoriais de dimensão finita

Base

Resumo das propriedades dos mapeamentos lineares injetivos e sobrejetivos

Um mapeamento linear entre espaços vetoriais de dimensão finita é determinado exclusivamente pelas imagens dos vetores de uma base . Se os vetores formam uma base do espaço vetorial e são vetores dentro , então há exatamente um mapeamento linear que mapeia em , em , ..., em . Se algum vetor estiver desativado , ele pode ser claramente representado como uma combinação linear dos vetores de base: ${\ displaystyle b_ {1}, \ dotsc, b_ {n}}$${\ displaystyle V}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle W}$${\ displaystyle f \ dois pontos V \ a W}$${\ displaystyle b_ {1}}$${\ displaystyle w_ {1}}$${\ displaystyle b_ {2}}$${\ displaystyle w_ {2}}$${\ displaystyle b_ {n}}$${\ displaystyle w_ {n}}$${\ displaystyle v}$${\ displaystyle V}$

${\ displaystyle v = \ textstyle \ sum \ limits _ {j = 1} ^ {n} v_ {j} b_ {j}}$

Aqui estão as coordenadas do vetor em relação à base . Sua imagem é dada por ${\ displaystyle v_ {1}, \ ldots, v_ {n}}$${\ displaystyle v}$${\ displaystyle \ {b_ {1}, \ dotsc, b_ {n} \}}$${\ displaystyle f (v)}$

${\ displaystyle f (v) = \ textstyle \ sum \ limits _ {j = 1} ^ {n} v_ {j} f (b_ {j}) = \ sum \ limits _ {j = 1} ^ {n} v_ {j} w_ {j}.}$

O mapeamento é injetivo se e somente se os vetores de imagem da base forem linearmente independentes . É sobrejetora se, e somente se, abranger a área alvo . ${\ displaystyle f}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle W}$

Se um atribui a cada elemento de uma base de um vector de forma arbitrária, de modo que é possível com a fórmula acima a um mapeamento linear, esta atribuição claramente continuar. ${\ displaystyle b_ {1}, \ dotsc, b_ {n}}$${\ displaystyle V}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle W}$${\ displaystyle f \ dois pontos V \ a W}$

Se os vetores de imagem são representados com referência a uma base de , isso leva à representação matricial do mapeamento linear. ${\ displaystyle w_ {j}}$${\ displaystyle W}$

Matriz de mapeamento

São e finito, , , e são bases de e a partir de onde, cada mapeamento linear pode por um - matriz são apresentados. Isso é obtido da seguinte forma: Para cada vetor de base de , o vetor de imagem pode ser representado como uma combinação linear dos vetores de base : ${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle \ dim V = n}$${\ displaystyle \ dim W = m}$${\ displaystyle B = \ {b_ {1}, \ dotsc, b_ {n} \}}$${\ displaystyle V}$${\ displaystyle B '= \ {b_ {1}', \ dotsc, b_ {m} '\}}$${\ displaystyle W}$${\ displaystyle f \ dois pontos V \ a W}$${\ displaystyle m \ times n}$ ${\ displaystyle M_ {B '} ^ {B} (f)}$${\ displaystyle b_ {j}}$${\ displaystyle B}$${\ displaystyle f (b_ {j})}$${\ displaystyle b_ {1} ', \ dotsc, b_ {m}'}$

${\ displaystyle f (b_ {j}) = \ sum _ {i = 1} ^ {m} a_ {ij} b_ {i} '}$

A , , são as entradas da matriz : ${\ displaystyle a_ {ij}}$${\ displaystyle i = 1, \ dotsc, m}$${\ displaystyle j = 1, \ dotsc, n}$${\ displaystyle M_ {B '} ^ {B} (f)}$

${\ displaystyle M_ {B '} ^ {B} (f) = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1j} & \ dots & a_ {1n} \\\ vdots && \ vdots && \ vdots \\ a_ {m1} & \ dots & a_ {mj} & \ dots & a_ {mn} \ end {pmatrix}}}$

A -ésima coluna contém as coordenadas de em relação à base . ${\ displaystyle j}$${\ displaystyle f (b_ {j})}$${\ displaystyle B '}$

Com a ajuda desta matriz pode-se calcular o vetor imagem de cada vetor : ${\ displaystyle f (v)}$${\ displaystyle v = v_ {1} b_ {1} + \ dotsb + v_ {n} b_ {n} \ in V}$

${\ displaystyle f (v) = \ sum _ {j = 1} ^ {n} v_ {j} f (b_ {j}) = \ sum _ {j = 1} ^ {n} v_ {j} \ left (\ sum _ {i = 1} ^ {m} a_ {ij} b_ {i} '\ direita) = \ sum _ {i = 1} ^ {m} \ esquerda (\ sum _ {j = 1} ^ {n} a_ {ij} v_ {j} \ right) b_ {i} '}$

Para as coordenadas de respeito tão verdadeiras ${\ displaystyle w_ {1}, \ dotsc, w_ {m}}$${\ displaystyle f (v)}$${\ displaystyle B '}$

${\ displaystyle w_ {i} = \ sum _ {j = 1} ^ {n} a_ {ij} v_ {j}}$.

Isso pode ser expresso com a ajuda da multiplicação da matriz:

${\ displaystyle {\ begin {pmatrix} w_ {1} \\\ vdots \\ w_ {m} \ end {pmatrix}} = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1n} \\\ vdots && \ vdots \\ a_ {m1} & \ dots & a_ {mn} \ end {pmatrix}} \, {\ begin {pmatrix} v_ {1} \\\ vdots \\ v_ {n} \ end {pmatrix} }}$

A matriz é chamada de matriz de mapeamento ou matriz de representação de . Outras grafias para são e . ${\ displaystyle M_ {B '} ^ {B} (f)}$${\ displaystyle f}$${\ displaystyle M_ {B '} ^ {B} (f)}$${\ displaystyle _ {B '} f_ {B}}$${\ displaystyle _ {B '} [f] _ {B}}$

Fórmula dimensional

Imagem e núcleo estão relacionados por meio do conjunto de dimensões. Isso afirma que a dimensão é igual à soma das dimensões da imagem e do núcleo: ${\ displaystyle V}$

${\ displaystyle \ dim V = \ dim \ mathrm {ker} (f) + \ dim \ mathrm {im} (f)}$

Mapeamentos lineares entre espaços vetoriais de dimensão infinita

Em análise funcional em particular , considera-se mapeamentos lineares entre espaços vetoriais de dimensão infinita. Nesse contexto, os mapeamentos lineares são geralmente chamados de operadores lineares. Os espaços vetoriais considerados em sua maioria ainda possuem a estrutura adicional de um espaço vetorial completo normalizado . Esses espaços vetoriais são chamados de espaços de Banach . Em contraste com o caso de dimensão finita, não é suficiente investigar operadores lineares apenas em uma base. De acordo com o teorema da categoria de Baier , uma base de um espaço de Banach infinitamente dimensional tem um número incontável de elementos e a existência de tal base não pode ser justificada construtivamente, ou seja, usando apenas o axioma da escolha . Um termo básico diferente é, portanto, usado, como bases ortonormais ou, mais geralmente, bases de tremor . Isso significa que certos operadores, como os operadores de Hilbert-Schmidt, podem ser representados usando "matrizes infinitamente grandes", em que combinações lineares infinitas também devem ser permitidas.

Mapas lineares especiais

Monomorfismo

Um monomorfismo entre espaços vector é um mapeamento linear que é injetivo . Este é o caso se os vetores de coluna da matriz de representação forem linearmente independentes.${\ displaystyle f \ dois pontos V \ a W}$

Epimorfismo

Um epimorfismo entre espaços vetoriais é um mapeamento linear que é sobrejetivo . Este é o caso se e somente se a classificação da matriz de representação for igual à dimensão de .${\ displaystyle f \ dois pontos V \ a W}$${\ displaystyle W}$

Isomorfismo

Um isomorfismo entre espaços vetoriais é um mapeamento linear que é bijetivo . Este é exatamente o caso quando a matriz de exibição é regular . Os dois espaços e são então chamados isomorphic.${\ displaystyle f \ dois pontos V \ a W}$${\ displaystyle V}$${\ displaystyle W}$

Endomorfismo

Um endomorfismo entre espaços vector é um mapa linear, em que os espaços e são iguais a: . A matriz de representação desta figura é uma matriz quadrada.${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle f \ dois pontos V \ a V}$

Automorfismo

Um automorfismo entre espaços vetoriais é um mapeamento linear bijetivo no qual os espaços e são iguais. Portanto, é um isomorfismo e um endomorfismo. A matriz de exibição desta figura é uma matriz regular.${\ displaystyle V}$${\ displaystyle W}$

Espaço vetorial de figuras lineares

Formação do espaço vetorial L (V, W)

O conjunto de mapeamentos lineares de um espaço vetorial para um espaço vetorial é um espaço vetorial final , mais precisamente: um subespaço do espaço vetorial de todos os mapeamentos de a . Isso significa que a soma de dois mapas lineares e , definidos por componentes por ${\ displaystyle L (V, W)}$${\ displaystyle K}$${\ displaystyle V}$${\ displaystyle K}$${\ displaystyle W}$${\ displaystyle K}$${\ displaystyle K}$${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle f}$${\ displaystyle g}$

${\ displaystyle (f + g) \ dois pontos x \ mapsto f (x) + g (x),}$

novamente é um mapeamento linear e que o produto

${\ displaystyle (\ lambda f) \ dois pontos x \ mapsto \ lambda f (x)}$

um mapeamento linear com um escalar também é um mapeamento linear novamente. ${\ displaystyle \ lambda \ in K}$

Se a dimensão e a dimensão são fornecidas em uma base e uma base , o mapeamento é ${\ displaystyle V}$${\ displaystyle n}$${\ displaystyle W}$${\ displaystyle m}$${\ displaystyle V}$${\ displaystyle B}$${\ displaystyle W}$${\ displaystyle C}$

${\ displaystyle L (V, W) \ a K ^ {m \ times n}, \ f \ mapsto M_ {C} ^ {B} (f)}$

um isomorfismo no espaço da matriz . O espaço vetorial, portanto, tem a dimensão . ${\ displaystyle K ^ {m \ vezes n}}$${\ displaystyle L (V, W)}$${\ displaystyle m \ cdot n}$

Se considerarmos o conjunto de auto-mapeamentos lineares de um espaço vetorial, ou seja, o caso especial , então estes não apenas formam um espaço vetorial, mas também uma álgebra associativa com a concatenação de mapeamentos como multiplicação , que é brevemente referida como. ${\ displaystyle V = W}$${\ displaystyle L (V)}$

generalização

Um mapeamento linear é um caso especial de um mapeamento afim .

Se o corpo for substituído por um anel na definição do mapeamento linear entre espaços vetoriais , um homomorfismo de módulo é obtido .

Notas e referências individuais

1. ↑ Às vezes, esse conjunto de mapeamentos lineares também é escrito como.${\ displaystyle {\ text {Hom}} _ {K} (V, W)}$

literatura

• Albrecht Beutelspacher : Linear Algebra. Uma introdução à ciência de vetores, mapas e matrizes. 6ª edição revisada e complementada. Vieweg Braunschweig et al., 2003, ISBN 3-528-56508-X , pp. 124-143.
• Günter Gramlich: Linear Algebra. Uma introdução para engenheiros. Fachbuchverlag Leipzig em Carl-Hanser-Verlag, Munich 2003, ISBN 3-446-22122-0 .
• Detlef Wille: Repetition of Linear Algebra. Volume 1. 4ª edição, reimpressão. Binomi, Springe 2003, ISBN 3-923923-40-6 .

Links da web